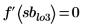Example: Optimizing a Function
Use the maximize and minimize functions, plus a guess value, to find the point at which the input function is at its maximum or minimum. The guess value tells the solver function to converge on a local maximum or minimum instead of other possible maxima or minima points. When you use the solver functions inside a solve block you can provide constraints that allow you to limit the search algorithm to a specific domain or to a specific region of the plot.
Using a Guess Value with no Constraints
1. Use the sin function to define an increasing sinusoidal function.
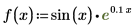 |
2. Use the maximize and minimize functions to find the local maximum and minimum given a guess value.
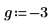 |
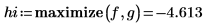 |
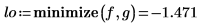 |
3. Plot the function and use vertical markers to show the local maximum and minimum.
 |
 |
 |
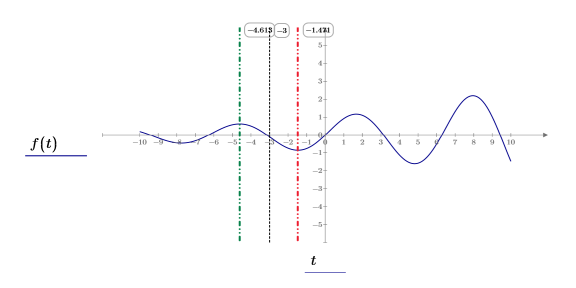
The functions return the local maximum and minimum that are closest to the guess value.
Using a Guess Value with an Unbounded Constraint
1. To place constraints on the maximize and minimize functions, use each function inside its own solve block.
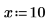 | 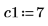 |
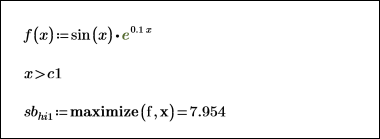
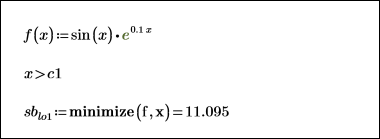
2. Use this short program to highlight the constraint region on a plot.
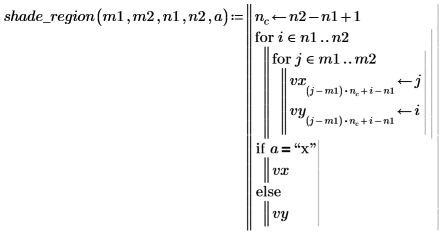
3. Set the start of the highlighted region to the value of the constraint, then generate the shading vectors.
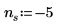 | 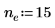 | 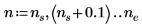 |
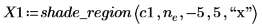 | ||
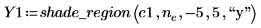 |
4. Show the shaded constraint region, the new guess value, and the new local maximum and minimum. Set the Line Style for the Y1 trace to (none).
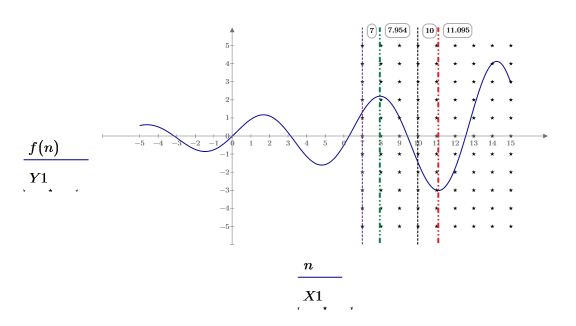
The returned minimum and maximum satisfy the constraint value of x>7.
Using a Guess Value with a Bounded Constraint
1. To place stricter constraints on the maximize and minimize functions, specify a lower and an upper limit on the constraint.
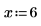 | 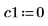 | 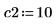 |
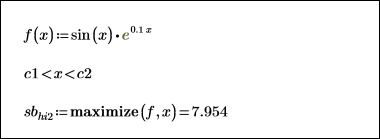
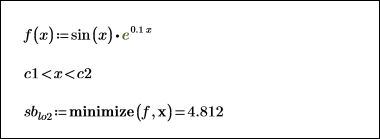
2. Set the start of the highlighted region to the value of the constraints, then generate the shading vectors.
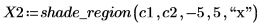 |
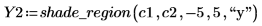 |
3. Show the shaded constraint region, the guess value, and the local maximum and minimum.
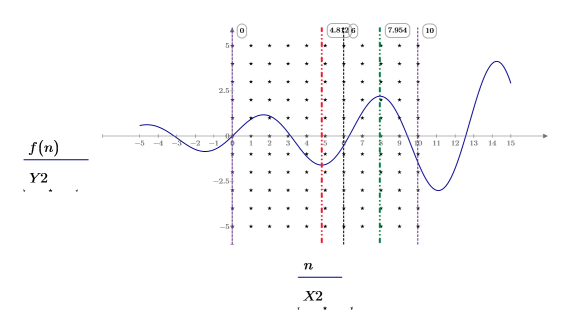
The returned minimum and maximum satisfy the constraint range of 0<x<10.
Caution when Using Constraints
When using constraints, it is advisable to verify that the returned minimum or maximum values are not equal to a constraint value.
1. Specify a narrowly bounded constraint and recalculate the minimum and maximum values.
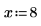 | 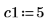 | 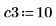 |
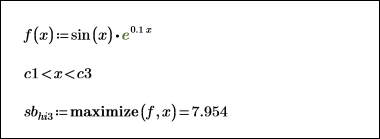

2. Set the start and end of the highlighted region to the lower and upper limits of the constraint, then generate the shading vectors.
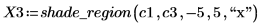 |
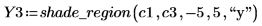 |
3. Show the shaded constraint region, the guess value, and the local maximum and minimum.
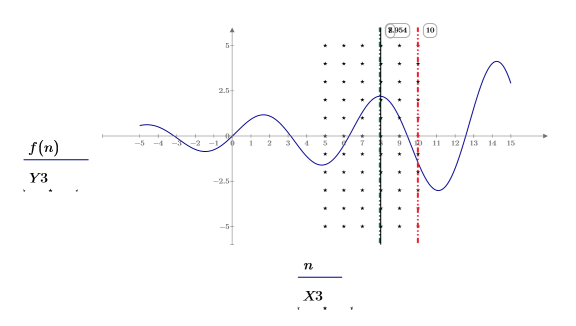
The returned maximum remains unchanged, but the returned minimum now equals the upper limit of the constraint. The returned minimum satisfies the constraint but does not fall on one of the function's minimal points. This implies that the minimize and maximize functions return the minimum and maximum values that satisfy the constraint but not necessarily the minima or maxima of the function.
In this case, the user is advised to relax the constraint until the returned values fall safely within the specified constraint and away from its limits.
4. On the Math Formatting tab, in the Results group, set the Result Format to (Decimal) and then check the validity of the returned minimum and maximum values by ensuring that evaluating the derivative of the input function at the returned values returns a zero.
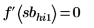 | 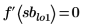 | 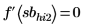 |
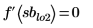 | 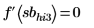 | 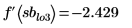 |
This shows that all the solve block calculated maximums and minimums cross the function curve at the correct maximum and minimum points except minimum sblo3.
5. Relax the upper limit of the constraint and recalculate the minimum and maximum points.
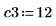
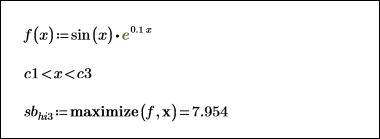
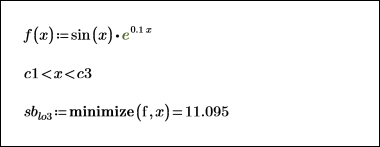
The minimum now falls well within the constraint region.