Example: Multiple Regression Predictor Retention Analysis
Use DOE functions and programs to find statistically significant regressions. Use the brute force approach where every combination of factors is tested. This is a difficult task reserved for advanced statistical applications. In PTC Mathcad, you can use recursive functions to ensure that every single combination is included while still minimizing the length of your programs.
1. Define a set of experimental data.

2. Extract the number of factors from Data.
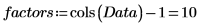
The number of potential regressions for this experiment is as follows:
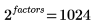
3. Extract the header row.
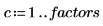
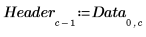
4. Extract the failure rates (Y) and the potential factors (X).
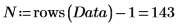
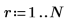
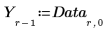
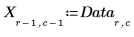
5. Use functions rows and concat to create a program for finding terms to use when testing regressions.

For example, for the factors "A", "B", and "C", the terms are:
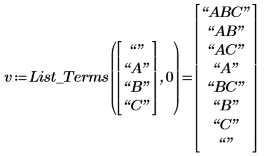
◦ The first argument of List_Terms is a vector that starts with an empty string to account for the regression constant followed by the names of all the factors.
◦ The second argument must start at 0. It is used by the program loops recursively until the desired outcome is reached.
◦ The terms returned are a selection of all the possible factor combinations. For example, CBA or ACB are omitted as using them in regressions would produce the same result as ABC.
6. Use functions rows and vec2str to create a program for mapping terms to single characters. The returned list is used as a reference so that terms can be retrieved later.

The first column of the returned list contains characters and the second column contains the corresponding terms.
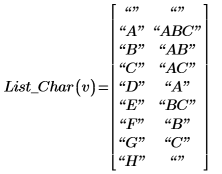
7. Use functions rows, strlen, match, and substr to create programs for reducing terms and the experimental data.


8. Create a program for determining whether the regression generated by the polyfitstat function meets your requirements, both in terms of significance (P) and of how well the regression describes the data (R2).

9. Create a program for formatting the regression results. The program returns the original term names as well as R2 and P for further sorting when all the regressions are identified.

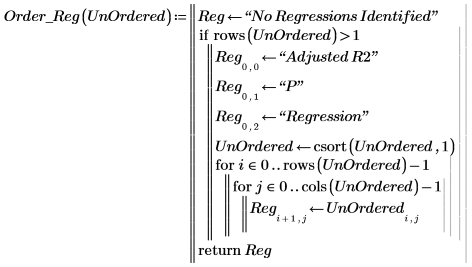
10. Create a program for ordering the results by the overall regression significance (P).
11. Use function polyfitstat to create a program for processing the regression analysis. This short but powerful program performs the following tasks:
◦ Finding all combinations of predictors.
◦ Iterating through all combinations of predictors and creating a regression for each combination.
◦ Testing whether the regressions met the supplied requirements.
◦ Formatting the valid regressions.
◦ Ordering the formatted regressions.

12. Call program Reg for processing the regression analysis.
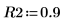
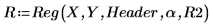
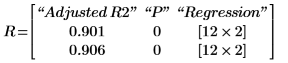
This program can take a significant amount of time before it returns an outcome, especially if the number of regression increases (for instance, if you increase the significance level). In this case, the program returns two regressions that meet the requirements defined by α and R2.
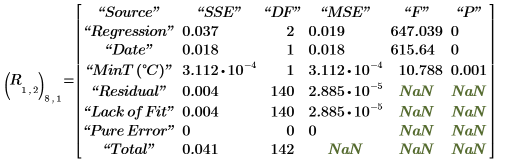
13. View some of the results of the regression analysis.
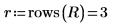



14. Define f to be the Standard Regression Equation.
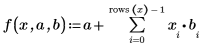
15. Redefine f so that it takes the coefficients of regression returned by Reg.
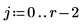
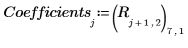
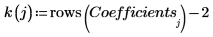
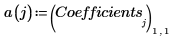
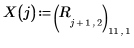
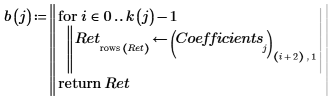
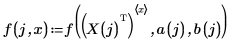
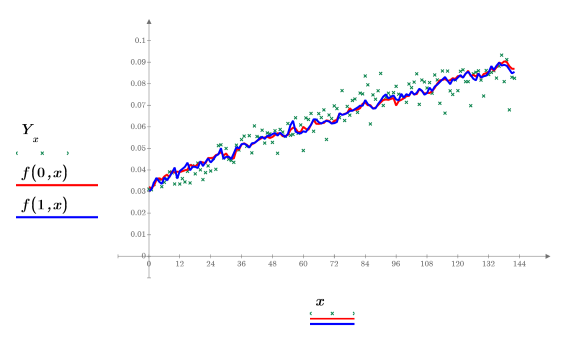
16. Plot the experimental data and the regressions.
Reference
Philip Leitch, BSc (Applied Biology/Environmental Science Hons), MBA (Hons)