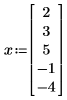
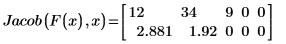Example: The Jacob Function
Use the Jacob function to compute the Jacobian of a vector function, written as a column vector of real-valued functions.
1. Define the two functions contained within vector F:
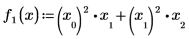
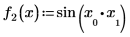
2. Define vector F:
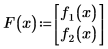
3. Since the variables are undefined numerically, evaluate Jacob symbolically.
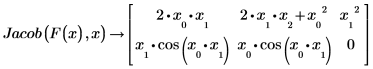
◦ Row 0 of the matrix contains three elements: the partial derivative of f1 with respect to x0, the partial derivative with respect to x1, and the partial derivative with respect to x2.
◦ Similarly, row 1 contains three elements: the partial derivative of f2 with respect to x0, the partial derivative with respect to x1, and the partial derivative with respect to x2.
PTC Mathcad assumes that the number of variables equals maxsub + 1, where maxsub is the largest subscript appearing among the variables in the functions. |
4. Assign numerical values to the variables, and then evaluate the Jacob function numerically:
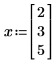
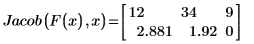
Specifying Additional Variables That Do Not Appear in the Functions
1. Force the resulting matrix to contain more columns than the number of variables by setting the optional third argument of Jacob:
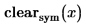
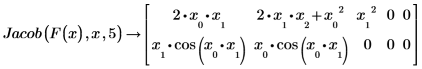
2. Force the resulting matrix to contain more columns than the number of variables by providing values to non-existing variables: