Example: IIR Filter Design
Use functions bessel, butter, cheby1, cheby2, iirlow, iirhigh, iirpass and iirstop to generate coefficients for an analog lowpass filter of the given type. Use the coefficients as arguments to one of the iir functions, which scale and perform bilinear transformation to produce the required frequency response.
|
|
• For lowpass and highpass filters with even order N, all sections are second-order, with three coefficients in each column. If the order is odd, the last section is first-order. For bandpass and bandstop filters, the conversion to a digital filter doubles the order of each section.
• Functions gain and response accept coefficient arrays in the form produced by these functions. Complex gain is found by multiplying section gains, and response by feeding each section's response into the next section.
• These functions implement algorithms in Chapter 7 of Signal Processing Algorithms by Samuel Stearns and Ruth David (Prentice-Hall, Inc.).
|
Lowpass Chebyshev Type I Filter
1. Define the order, the ripple parameter, and the cutoff frequency.
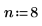
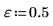
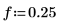
2. Use functions iirlow and cheby1 to generate the filter coefficients.
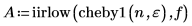

Filter A has four quadratic sections. |
3. Plot the magnitude of the gain, and use a horizontal marker to mark the ripple level.
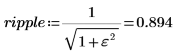
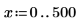
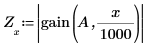
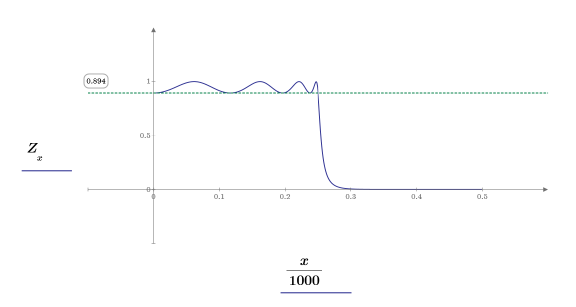
Since the transfer function is given as a product of quadratic factors, plotting the poles on the complex plane becomes straightforward.
4. Find the complex roots of each factor of the denominator.
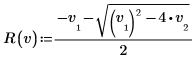
The poles of the transfer function of filter A are the roots of quadratics with coefficients given by the odd-numbered columns of A, with the coefficient of the quadratic term first. |
5. Find one root for each factor of the denominator.
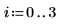
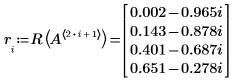
6. Fill in the conjugate roots.
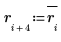
7. Show the transfer function poles and plot them on the complex plane. Add a unit circle trace for reference.
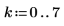

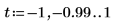
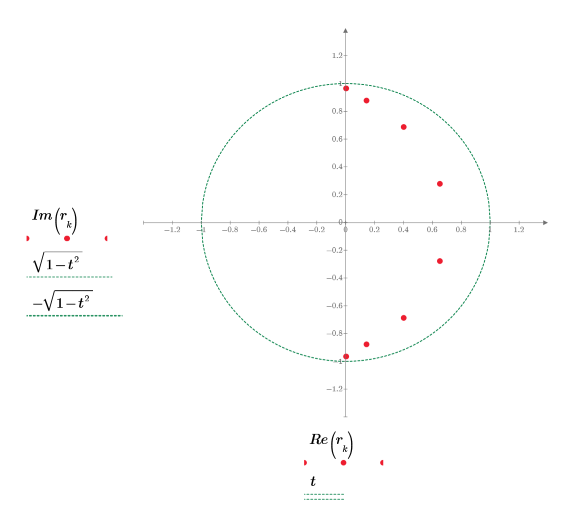
The plot shows that all eight poles are inside the unit circle, so the filter is stable, as required.
8. Use function max to numerically verify that all eight poles fall inside the unit circle.
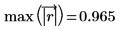
9. Apply the response function then plot the impulse response of filter A. Give it a vector of length 1 representing a unit impulse as the first argument.
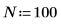
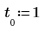
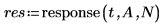
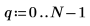
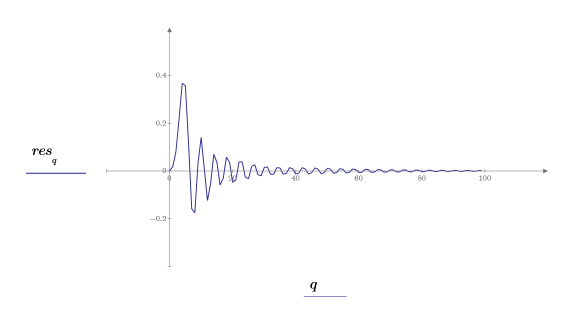
Although the response is infinite in length, it drops to nearly 0 after the first 80 terms. The stability condition guarantees that the sum of the absolute values of the response is bounded.
Lowpass Chebyshev Type II Filter
1. Set the parameters for a Type II Chebyshev filter.
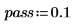
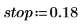
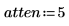
2. Use function tan to compute the scale.
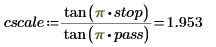
See Stearns and David for the theory behind this computation; this number will always be greater than 1. |
3. Use the iirlow and cheby2 functions to calculate the coefficients for a fifth-order, lowpass, IIR filter with cutoff frequency f=pass.
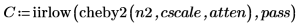

The coefficient matrix has two quadratic sections and one linear section. |
4. Use function gain to compute the gain at each frequency, then plot the frequency response. Use markers to show the pass and stop frequencies, and the inverse of attenuation level.
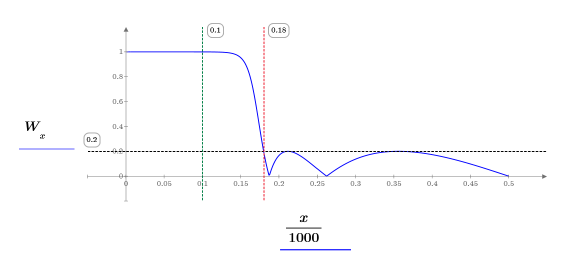
The response plot shows how well the design criteria are met. The markers help in seeing that the stopband begins at the required location (the intersection of the stop and 1/atten lines) and that the passband ends to the right of the cutoff frequency.
5. Use the iirlow and cheby2 functions to repeat the above design while using a larger attenuation.
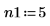
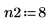
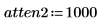
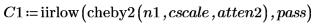
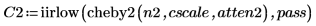
Higher attenuations require higher order filters in order to get the transition band down to the required width. Try a five-order and an eight-order filters and compare the results. |
6. Plot the gain of a five-order filter in dB. Use markers to mark the pass frequency and the desired 30 dB attenuation.
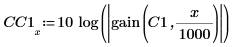
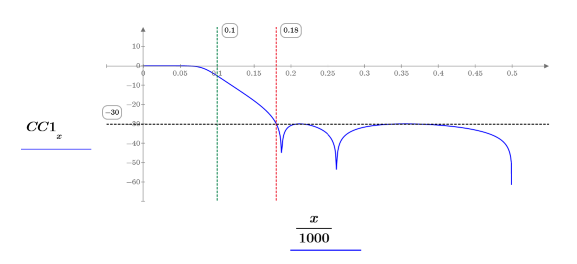
7. Plot the gain of an eight-order filter in dB. Use markers to mark the pass frequency and the desired 30 dB attenuation.
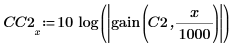
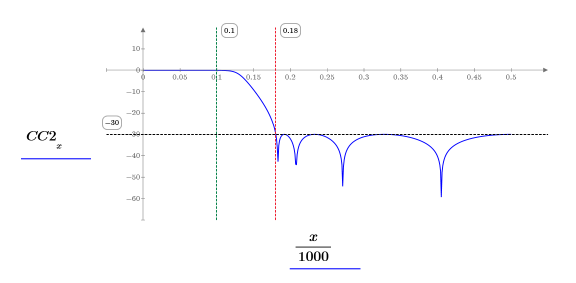
While the gain below the -30db line is similar around the stop frequency for both filters, the gain of the eight-order filter remains flat beyond cutoff frequency. This means that an eight-order filter is required to achieve the desired attenuation of 1000.
Computing the Scale Factor
The equations below show the definition of the scale factor for the highpass, bandpass and bandstop filters.
• Highpass filter:
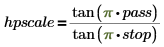
• Bandpass filter:
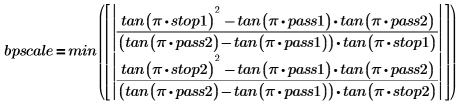
Parameters pass1 and pass2 are the lower and upper edges of the passband, and parameters stop1 and stop2 are the edges of the two stopbands.
• Bandstop filter:
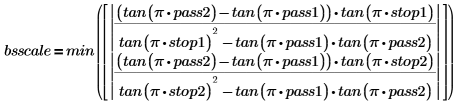
Parameters pass1 and pass2 are the edges of the two passbands, and parameters stop1 and stop2 are the lower and upper edges of the stopband.
1. Define the parameters for a bandpass filter:
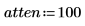
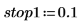
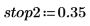
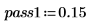
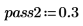
2. Compute the scale of a bandpass filter using the above parameters.
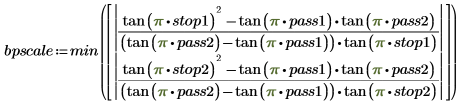
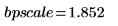
3. Compute the coefficients for the above bandpass filter.
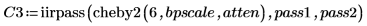

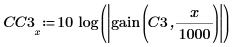
4. Plot the response in dB and show the stop and pass markers.
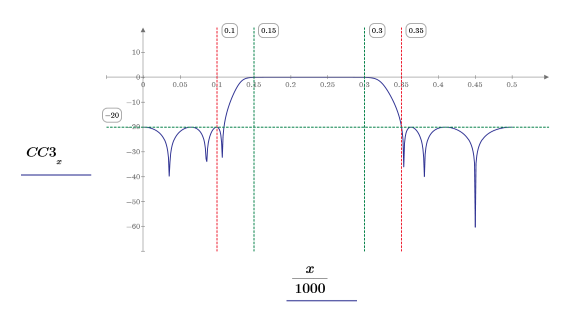
The right stopband edge falls exactly at the correct location, but the left stopband edge rises just above the target frequency value. This means that this transition band is narrower than required.
Lowpass Bessel Filter
A Bessel filter is returned as a single section.
1. Set the Bessel filter parameters.
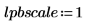
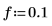
The scale parameter can be used to control the gain at the cutoff frequency. |
2. Use the bessel function to calculate the Bessel filter coefficients.
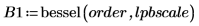
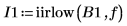

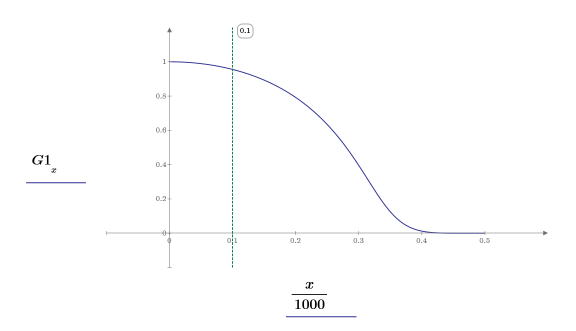
3. Plot the gain and show the gain at the cutoff frequency.
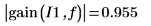
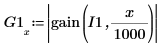
4. Trade the lower gain at the cutoff frequency for increased attenuation in the stopband using the scaling factor.
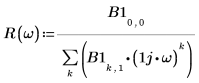
R is the analog transfer function corresponding to the analog coefficients B1.
5. Use the root function, with a starting guess value of 1, to find the point at which the analog transfer function R equals 0.8 at the cutoff frequency.
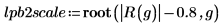
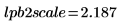
The scale marker crosses the gain curve at 0.8.
The guess value must be a positive number such that it results in a positive scale value. |
6. Recompute the digital filter coefficients using the calculated scale factor.
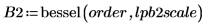
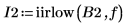
7. Plot the new frequency response and show the gain at the cutoff frequency.
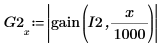
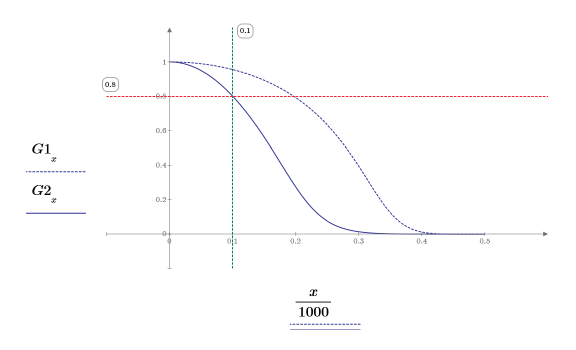
The plot shows that the new frequency response has a sharper transition to zero past the cutoff frequency. Using the scale factor results in increased attenuation in the stopband.
Bandpass, Bandstop, and Highpass Butterworth Filters
The order of the input coefficients is doubled by the iirpass and iirstop functions, so fourth-order analog coefficients result in an eighth-order filter.
Bandpass Butterworth Filter
1. Set the filter parameters.
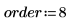
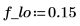
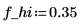
2. Compute the coefficients.
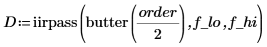
3. Plot the response. Use vertical markers to show the low and high frequencies.
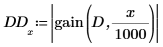
The response shows that frequencies between f_lo and f_hi are allowed to pass. All others are filtered out.
Bandstop Butterworth Filter
1. Set the filter order.
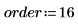
2. Use the iirstop and butter functions to compute the coefficients.
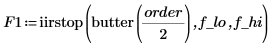
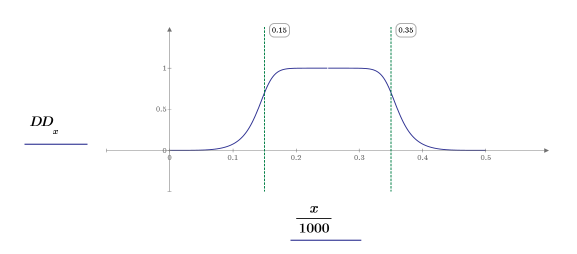
3. Plot the response. Use vertical markers to show the low and high frequencies.
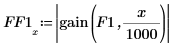
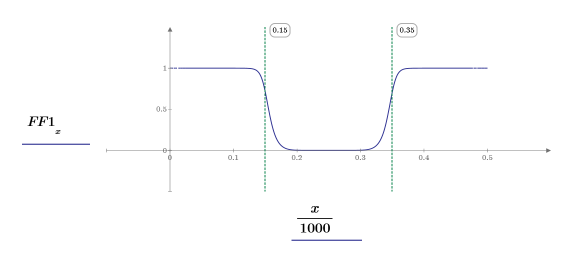
The response shows that frequencies between f_lo and f_hi are stopped from going through. All others are allowed to pass.
Highpass Butterworth Filter
1. Set the filter order.
2. Use the iirhigh and butter functions to compute the coefficients.

Unlike the iirpass and iirstop functions, the iirhigh function does not double the order of the input coefficients. Therefore, the order value was passed as is to the butter function. |
3. Plot the response. Use a vertical marker to show the high frequency.
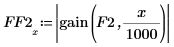
The response shows that frequencies that are higher than f_hi are allowed to pass. All others are filtered out.