Symbolische Gamma-Funktionen
• Psi(z) – Gibt die Ableitung des natürlichen Logarithmus der Gamma-Funktion Γ(z) zurück. Die Digamma-Funktion ist wie folgt definiert:

• Psi(n, z) – Gibt die nth Ableitung von Psi(z) zurück. Die Polygamma-Funktion ist wie folgt definiert:
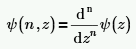
Zwischen Psi(z) und Psi(n, z) besteht folgende Beziehung:
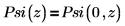
Argumente
• z ist ein reeller oder komplexer Skalar oder ein Vektor von reellen oder komplexen Skalaren.
• n ist eine nicht negative Ganzzahl.
Zusätzliche Informationen
• Sie können die Variante der Funktion Psi, die über nur ein Argument verfügt, sowohl symbolisch als auch numerisch auswerten. Wenn Sie sie numerisch auswerten, kann z auch ein komplexer Skalar oder ein Vektor von komplexen Skalaren sein.
• Sie können die 2-Argument-Version der Funktion Psi nur symbolisch auswerten.