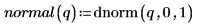Beispiel: Z-Score eines Datenvektors
Berechnen Sie ein z-Score für einen Vektor oder normal verteilte Daten mit einer bekannten Standardabweichung der Grundgesamtheit.
1. Legen Sie einen zu analysierenden Datensatz fest.

2. Berechnen Sie den Stichprobenmittelwert m_s.
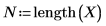
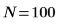
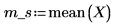
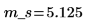
3. Definieren Sie das Signifikanzniveau, die Standardabweichung der Grundgesamtheit und den vorgeschlagenen Mittelwert der Grundgesamtheit.
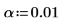
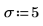
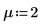
4. Berechnen Sie das z-Score.
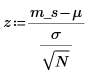
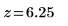
5. Legen Sie die Null- und die Alternativhypothese für einen zweiseitigen Test fest.
H0: m = μ
H1: m ≠ μ
6. Verwenden Sie die Funktion pnorm, um den p-Wert zu berechnen und die Hypothese zu prüfen. In diesem Beispiel werden alle Booleschen Ausdrücke mit 1 ausgewertet, wenn die Nullhypothese wahr ist (H0 wird nicht zurückgewiesen).
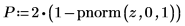
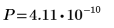
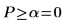
Die Wahrscheinlichkeit, dass die Teststatistik größer ist als die beobachtete, beträgt 4.11*10-10, falls die Nullhypothese wahr ist. Der Vergleich zwischen dem p-Wert und dem Signifikanzniveau gibt an, dass es einen Anhaltspunkt dafür gibt, dass die alternative Hypothese wahr ist.
7. Verwenden Sie die Funktion qnorm, um die Grenzwerte des kritischen Bereichs zu berechnen und die Hypothese zu prüfen.
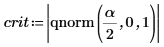
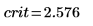
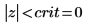
Lehnen Sie die Nullhypothese ab. Es gibt Anhaltspunkte dafür, dass der Mittelwert ungleich μ ist.
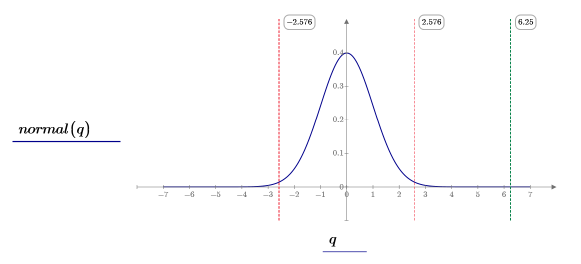
8. Verwenden Sie die Funktion dnorm, um die standardmäßige Normalverteilung (blau), die Grenzen des kritischen Bereichs (rot) und das z-Score (grün) zu berechnen und zu plotten.