Beispiel: Varianz und Standardabweichung
Verwenden Sie die Funktionen Var und Stdev, um die Streuung einer Weibull- und einer Normalverteilung zu vergleichen.
1. Definieren Sie Datensätze mit einer Weibull- und einer Normalverteilung.
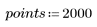
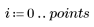
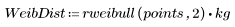
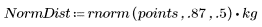
2. Plotten Sie die Verteilungen.
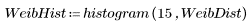
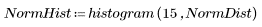
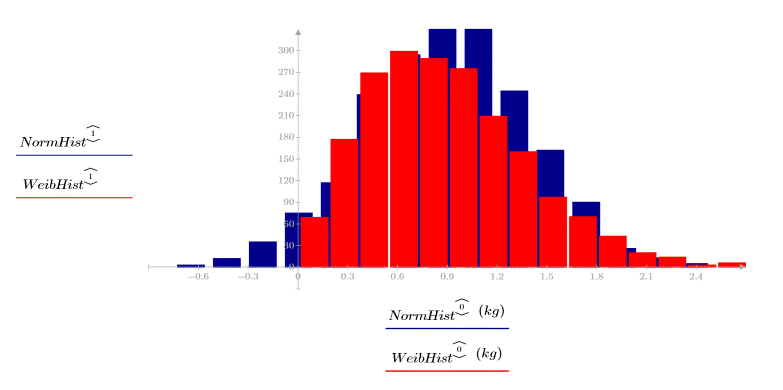
Die beiden Datensätze haben unterschiedliche Streuungen und Formen, auch wenn ihre Mittelwerte ähnlich sind:
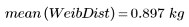
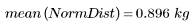
3. Berechnen Sie die Stichproben-Varianz der Verteilungen.
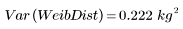

Die geringere Varianz der Weibull-Verteilung zeigt an, dass deren Streuung kleiner ist als die der Normalverteilung.
Die Stichproben-Varianz wird wie folgt berechnet:
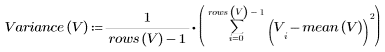
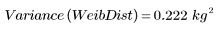
4. Berechnen Sie für die Stichproben die Standardabweichung der Weibull-Verteilung.
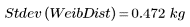
Da die Standardabweichung die gleichen Einheiten wie die ursprünglichen Daten hat, stellt sie ein etwas intuitiveres Maß der Streuung dar als die Varianz. Sie kann als Maß des Fehlers in einer Reihe von Messungen betrachtet werden, die eigentlich gleich sein sollten.
Die Standardabweichung der Stichproben ist die Quadratwurzel der Stichproben-Varianz:
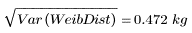
5. Berechnen Sie die Varianz der Grundgesamtheit und die Standardabweichungen für die Weibull-Verteilung:
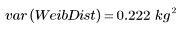
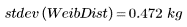
Die Varianz der Grundgesamtheit und die Standardabweichung werden durch die Stichprobengröße geteilt, nicht durch die Stichprobengröße minus 1:
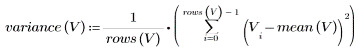
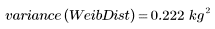
Die Stichproben-Varianz oder die Funktion Var ist die häufiger verwendete Definition bei der quantitativen Datenanalyse. |