Beispiel: T-Test auf normal verteilte Mittelwerte

Funktionen > Statistik > Wahrscheinlichkeitsverteilungen > Beispiel: T-Test auf normal verteilte Mittelwerte

Testen Sie die Hypothese, dass zwei normale Grundgesamtheiten gleiche Mittelwerte haben.

1. Definieren Sie zu vergleichende Datensätze.

2. Sammeln Sie die Stichprobenstatistik.

Anzahl der Stichproben für jeden Datensatz	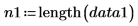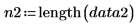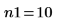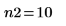<region id="ID0EJC1BB" top="403.20000000000005" left="38.400000000000006" width="137.98000000000002" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="91"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">n1</id> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">length</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data1</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0ESC1BB" top="441.60000000000008" left="38.400000000000006" width="137.98000000000002" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="95"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">n2</id> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">length</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data2</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EHD1BB" top="403.20000000000005" left="384.00000000000006" width="65.516666666666666" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="93"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0EVD1BB" top="441.60000000000008" left="384.00000000000006" width="65.516666666666666" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="97"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Mittelwerte der Stichproben	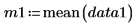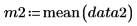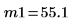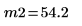<region id="ID0E1E1BB" top="480.00000000000006" left="38.400000000000006" width="136.66000000000003" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="99"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">m1</id> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">mean</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data1</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0EIF1BB" top="518.40000000000009" left="38.400000000000006" width="136.66000000000003" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="103"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">m2</id> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">mean</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data2</id> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E4F1BB" top="480.00000000000006" left="384.00000000000006" width="82.250000000000014" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="101"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m1</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0ELG1BB" top="518.40000000000009" left="384.00000000000006" width="82.250000000000014" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="105"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m2</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Standardabweichungen der Stichproben	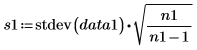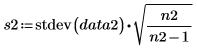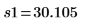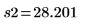<region id="ID0EQH1BB" top="614.40000000000009" left="38.400000000000006" width="197.0459999702374" height="50.065333527326587" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="111"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">s1</id> <apply> <mult /> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">stdev</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data1</id> </apply> <apply> <nthRoot /> <placeholder /> <apply> <div /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <apply> <minus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <real>1</real> </apply> </apply> </apply> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0E5H1BB" top="672.00000000000011" left="38.400000000000006" width="197.0459999702374" height="50.065333527326587" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="115"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="">s2</id> <apply> <mult /> <apply> <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">stdev</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">data2</id> </apply> <apply> <nthRoot /> <placeholder /> <apply> <div /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> <apply> <minus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> <real>1</real> </apply> </apply> </apply> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ETI1BB" top="614.40000000000009" left="384.00000000000006" width="90.876666666666679" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="113"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s1</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region> <region id="ID0EBJ1BB" top="672.00000000000011" left="384.00000000000006" width="90.876666666666679" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="117"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s2</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Freiheitsgrade bei der Kombination der beiden Mittelwerte	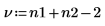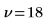<region id="ID0EGK1BB" top="556.80000000000007" left="38.400000000000006" width="105.12666666666667" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="107"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="*">ν</id> <apply> <minus /> <apply> <plus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> </apply> <real>2</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E2K1BB" top="556.80000000000007" left="384.00000000000006" width="56.493333333333339" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="109"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">ν</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
Standardfehler der Differenz der Datensätze	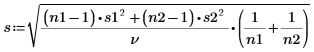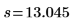<region id="ID0E5L1BB" top="729.60000000000014" left="38.400000000000006" width="313.71933330357075" height="52.217333527326588" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="119"> <define xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="*">s</id> <apply> <nthRoot /> <placeholder /> <apply> <mult /> <apply> <div /> <apply> <plus /> <apply> <mult /> <parens> <apply> <minus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> <real>1</real> </apply> </parens> <apply> <pow /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s1</id> <real>2</real> </apply> </apply> <apply> <mult /> <parens> <apply> <minus /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> <real>1</real> </apply> </parens> <apply> <pow /> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s2</id> <real>2</real> </apply> </apply> </apply> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">ν</id> </apply> <parens> <apply> <plus /> <apply> <div /> <real>1</real> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n1</id> </apply> <apply> <div /> <real>1</real> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n2</id> </apply> </apply> </parens> </apply> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ESM1BB" top="729.60000000000014" left="384.00000000000006" width="82.896666666666675" height="25.6" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="121"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">s</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

3. Definieren Sie das Signifikanzniveau.

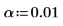
4. Berechnen Sie die Test-Statistik.

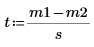
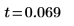
5. Legen Sie die Null- und die alternative Hypothese fest.

H0: m1 ≤ m2

H1: m1 > m2

6. Berechnen Sie den p-Wert, testen Sie die Hypothese. In diesem Beispiel werden alle Booleschen Ausdrücke mit 1 ausgewertet, wenn die Nullhypothese wahr ist (H0 wird nicht zurückgewiesen).

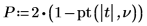
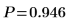
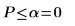
Die Wahrscheinlichkeit, dass die Teststatistik größer ist als die beobachtete, beträgt 0.016, falls die Nullhypothese wahr ist. Der Vergleich zwischen dem p-Wert und dem Signifikanzniveau zeigt, dass es keinen Anhaltspunkt dafür gibt, dass die alternative Hypothese wahr ist.

7. Berechnen Sie den Grenzwert des kritischen Bereichs, und testen Sie die Hypothese.

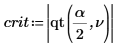
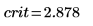
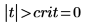
Akzeptieren Sie die Nullhypothese. Es gibt keinen Anhaltspunkt dafür, dass m1 größer ist als m2.

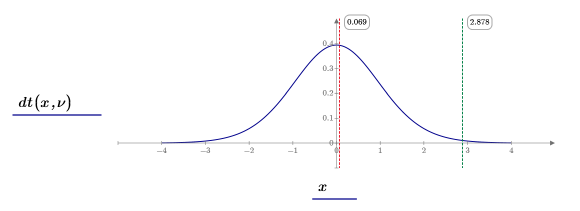
8. Plotten Sie die Student-Verteilung (blau), die Grenze des kritischen Bereichs (grün) und die Test-Statistik (rot).

<region id="ID0E5Y1BB" top="1804.8000000000002" left="38.400000000000006" width="580" height="211.19999999999996" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true" background-type="white">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace num-of-points="500" resultRef="141">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-4" end="4">
          <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">crit</id>
            <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">t</id>
          </markers>
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="152">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math resultRef="153">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="147">
              <real xmlns="http://schemas.mathsoft.com/math50">-4</real>
            </startValue>
            <real xmlns="http://schemas.mathsoft.com/math50">-3</real>
            <endValue resultRef="151">
              <real xmlns="http://schemas.mathsoft.com/math50">4</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.4">
          <axisLine position="origin" positionticmark="4" legendWidth="106.173333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="160">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id xml:space="preserve">dt</id>
                  <sequence>
                    <id xml:space="preserve">x</id>
                    <id xml:space="preserve">ν</id>
                  </sequence>
                </apply>
              </math>
              <math resultRef="161">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="155">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <real xmlns="http://schemas.mathsoft.com/math50">0.1</real>
            <endValue resultRef="159">
              <real xmlns="http://schemas.mathsoft.com/math50">0.4</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Zugehörige Themen

Student-t-Verteilung

War dies hilfreich?