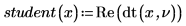Beispiel: T-Score eines Datenvektors
Berechnen Sie ein t-Score für einen Vektor normalverteilter Daten in Bezug auf einen bestimmten Mittelwert.
1. Definieren Sie einen zu analysierenden Datenvektor.

2. Sammeln Sie die Stichprobenstatistik.
Anzahl der Stichproben | 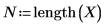 | 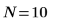 |
Mittelwert der Stichprobe | 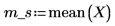 | 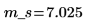 |
Standardabweichung der Stichprobe | 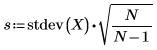 | 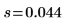 |
Standardfehler des Mittelwerts | 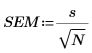 | 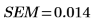 |
Freiheitsgrad | 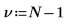 | 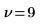 |
3. Definieren Sie das Signifikanzniveau und den vorgeschlagenen Mittelwert der Grundgesamtheit.
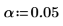
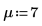
4. Berechnen Sie das t-Score.
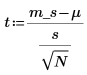
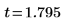
5. Legen Sie die Null- und die alternative Hypothese fest.
H0: m ≤ μ
H1: m > μ
6. Berechnen Sie den p-Wert, testen Sie die Hypothese.
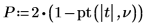
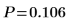
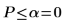
Die Wahrscheinlichkeit, dass die Teststatistik größer ist als die beobachtete, beträgt 0.016, falls die Nullhypothese wahr ist. Der Vergleich zwischen dem p-Wert und dem Signifikanzniveau zeigt, dass es keinen Anhaltspunkt dafür gibt, dass die alternative Hypothese wahr ist.
7. Berechnen Sie den Grenzwert des kritischen Bereichs, und testen Sie die Hypothese.
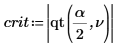
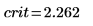
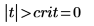
Akzeptieren Sie die Nullhypothese. Es gibt keinen Anhaltspunkt dafür, dass der Mittelwert größer ist als μ.
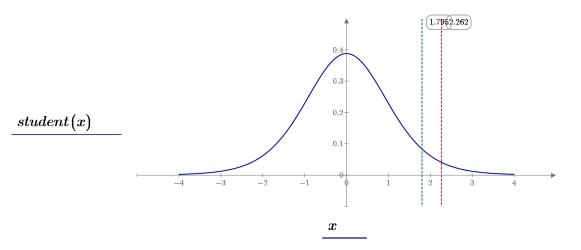
8. Plotten Sie die Student-t-Verteilung (blau), die Grenze des kritischen Bereichs (rot) und das t-Score (grün).