Beispiel: Thiele-Interpolation
Führen Sie an einem Datensatz eine Thiele-Kettenbruchinterpolation aus.
Thielecoeff und Thiele
Verwenden Sie die Funktionen Thielecoeff und Thiele, um einen von einer rationalen Funktion stammenden Datensatz zu interpolieren.
1. Definieren Sie die Anzahl der Interpolationspunkte.
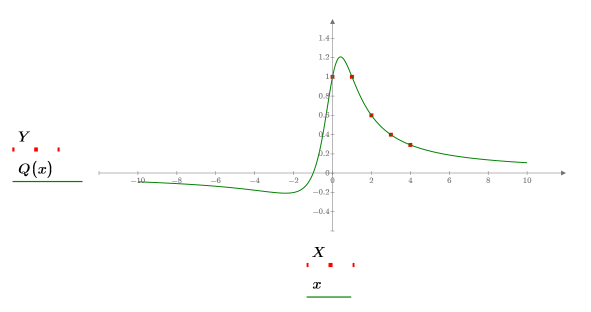
2. Definieren Sie eine rationale Funktion, beispielsweise die Funktion Lorentzian.
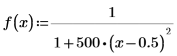
3. Nehmen Sie Samples der Funktion, und zeichnen Sie deren x- und y-Werte in Vektoren auf.
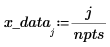
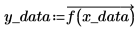
4. Suchen Sie mithilfe der Funktion Thielecoeff die Koeffizienten des Kettenbruchs, der zu den abgetasteten Punkten passt.
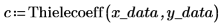
5. Rufen Sie die Funktion Thiele auf, um die Interpolation durchzuführen.
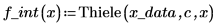
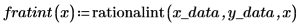
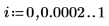
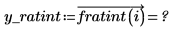
Die Funktionen Thiele funktionieren, die Funktion rationalint versagt jedoch an einigen Punkten in diesem Interpolationsbereich. Grund hierfür ist, dass die Daten symmetrisch sind, sodass bei einigen x-Zwischenwerten Fehler aufgrund einer Division durch null auftreten:
6. Plotten Sie die ursprüngliche Funktion, die abgetasteten Punkte und die interpolierte Kurve.
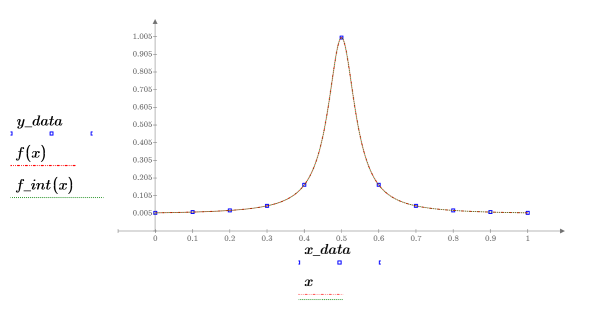
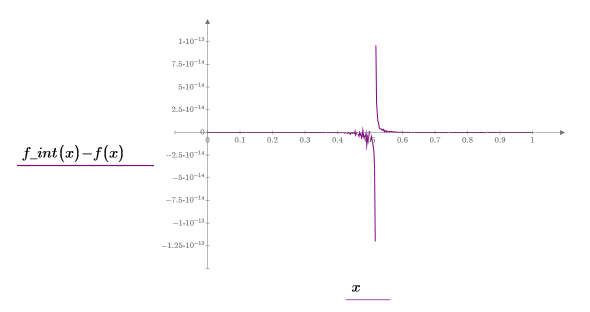
7. Plotten Sie einen Graphen, der die Residua für die Thiele-Interpolation zeigt.
Anordnung der Punkte
Der Algorithmus gibt nicht die richtigen Werte zurück, wenn zwei angrenzende Punkte identische y-Werte aufweisen. Sie müssen die Daten umordnen, um das richtige Ergebnis zu erhalten.
1. Definieren Sie einen Satz von Punkten.
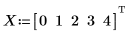
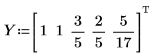
2. Suchen Sie die Koeffizienten der Thiele-Funktion.
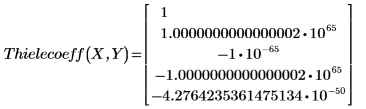
Die Koeffizienten sind zu groß.
3. Ordnen Sie die Daten um, um eine geeignete Lösung zu erhalten.
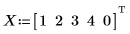
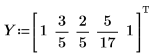
4. Wiederholen Sie Schritt 2.
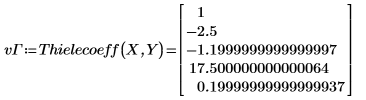
5. Definieren Sie die interpolierte Funktion.
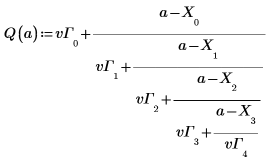
6. Plotten Sie die interpolierte Funktion und die ursprünglichen Datenpunkte.