Beispiel: Die Hartley-Transformation

Funktionen > Signalverarbeitung > Zusätzliche Transformationen > Beispiel: Die Hartley-Transformation

Verwenden Sie die Funktion dht, um die Hartley-Transformation von Signalen zu ermitteln.

Die definierende Summe der Hartley-Transformation entspricht der diskreten Summe der Fourier-Transformation.

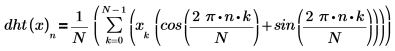
Dabei gilt: N ist die Anzahl der Elemente im reellen Daten-Array x.

Summe von Sinuskurven

Ermitteln Sie die Hartley-Transformation für eine Summe von Sinuswellen, und vergleichen Sie sie mit dem Betrag der komplexen Fourier-Transformation.

1. Legen Sie die Anzahl der Elemente fest.

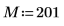
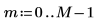
2. Verwenden Sie die Funktion sin, um das Eingangssignal zu definieren.

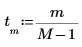
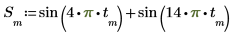
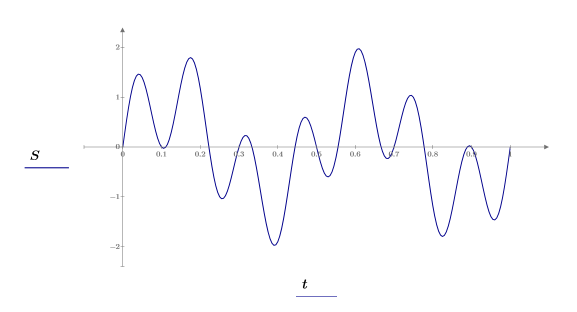
3. Plotten Sie das Signal.

<region id="ID0ENCX4" actualWidth="577.15384615384619" actualHeight="312" top="537.60000000000014" left="38.400000000000006" height="312" width="577.15384615384619" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="193">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="481.153846153846" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="1">
          <axisLine position="origin" positionticmark="2" legendWidth="58.32" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="196">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
              </math>
              <math resultRef="197">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue resultRef="195">
              <real xmlns="http://schemas.mathsoft.com/math50">1.0</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-2" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="61.6633333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="204">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">S</id>
              </math>
              <math resultRef="205">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="199">
              <real xmlns="http://schemas.mathsoft.com/math50">-2</real>
            </startValue>
            <secondTickValue resultRef="201">
              <real xmlns="http://schemas.mathsoft.com/math50">-1.0</real>
            </secondTickValue>
            <endValue resultRef="203">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

4. Verwenden Sie die Funktion dht, um die diskreten Frequenzen anzuzeigen, die in den beiden Sinuswellen dargestellt sind. Verwenden Sie dann die Funktion center, um die DC-Komponente in die Mitte zu verschieben.

<region id="ID0EPFX4" actualWidth="556.61538461538464" actualHeight="312" top="1017.6000000000001" left="38.400000000000006" height="312" width="556.61538461538464" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="218">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.615384615385" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-100" end="100">
          <axisLine position="origin" positionticmark="2" legendWidth="59.5966666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="221">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">f</id>
              </math>
              <math resultRef="222">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="220">
              <real xmlns="http://schemas.mathsoft.com/math50">-100</real>
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.6" end="0.6">
          <axisLine position="origin" positionticmark="5" legendWidth="67.37" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="227">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">hs</id>
              </math>
              <math resultRef="228">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="224">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.6</real>
            </startValue>
            <secondTickValue resultRef="226">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.3</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

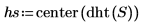
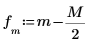
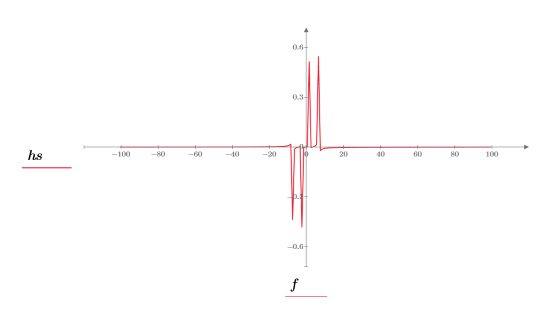
5. Verwenden Sie die Funktionen match und max, um die diskreten Frequenzen zu ermitteln, bei denen die Spitzen auftreten, und markieren Sie einen solchen Punkt mit einem vertikalen und einem horizontalen Markierer.

<region id="ID0EDIX4" actualWidth="234.18333333333334" actualHeight="36.800000000000004" top="1420.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="236">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">p1</id>
      <eval>
        <apply>
          <indexer />
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">match</id>
            <sequence>
              <apply>
                <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">max</id>
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">hs</id>
              </apply>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">hs</id>
            </sequence>
          </apply>
          <real>0</real>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ENJX4" actualWidth="557.95384615384614" actualHeight="235.2" top="1478.4000000000003" left="38.400000000000006" height="235.2" width="557.95384615384614" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="242">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="461.953846153846" height="177.6" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-20" end="20">
          <axisLine position="origin" positionticmark="2" legendWidth="59.5966666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="243" display="true" color="#FFFF0000" line-style="Dash" value="6.5">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">f</id>
                <id xml:space="preserve">p1</id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="249">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">f</id>
              </math>
              <math resultRef="250">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="246">
              <real xmlns="http://schemas.mathsoft.com/math50">-20</real>
            </startValue>
            <endValue resultRef="248">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.6" end="0.6">
          <axisLine position="origin" positionticmark="5" legendWidth="67.37" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="251" display="true" color="#FF008000" line-style="DashDotDot" value="0.547390503599252">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">hs</id>
                <id xml:space="preserve">p1</id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="259">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">hs</id>
              </math>
              <math resultRef="260">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="254">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.6</real>
            </startValue>
            <secondTickValue resultRef="256">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.3</real>
            </secondTickValue>
            <endValue resultRef="258">
              <real xmlns="http://schemas.mathsoft.com/math50">0.6</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

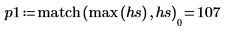
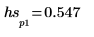
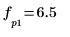
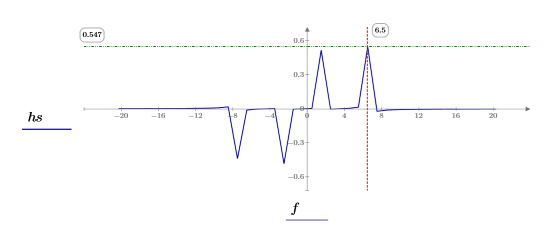
6. Verwenden Sie die Funktionen dft und center, um die diskrete Fourier-Transformation zu ermitteln und zu zentrieren.

<region id="ID0EQLX4" actualWidth="157.48666666666668" actualHeight="47.2" top="1785.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="272">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="*">dfts</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">center</id>
        <apply>
          <div />
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">dft</id>
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">S</id>
          </apply>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">M</id>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

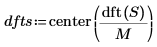
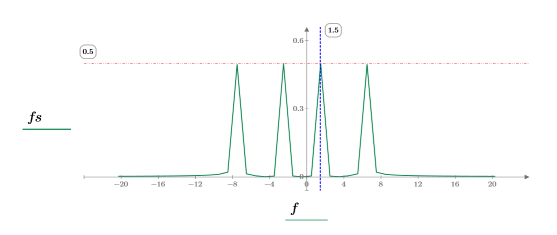
7. Plotten Sie die absoluten Werte der DFT.

<region id="ID0EONX4" actualWidth="556.61538461538464" actualHeight="312" top="1881.6000000000004" left="38.400000000000006" height="312" width="556.61538461538464" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="276">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.615384615385" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-100" end="100">
          <axisLine position="origin" positionticmark="0" legendWidth="59.5966666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="279">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">f</id>
              </math>
              <math resultRef="280">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="278">
              <real xmlns="http://schemas.mathsoft.com/math50">-100</real>
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.6">
          <axisLine position="origin" positionticmark="5" legendWidth="65.9166666666667" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="287">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">fs</id>
              </math>
              <math resultRef="288">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="282">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="284">
              <real xmlns="http://schemas.mathsoft.com/math50">0.3</real>
            </secondTickValue>
            <endValue resultRef="286">
              <real xmlns="http://schemas.mathsoft.com/math50">0.6</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

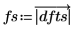
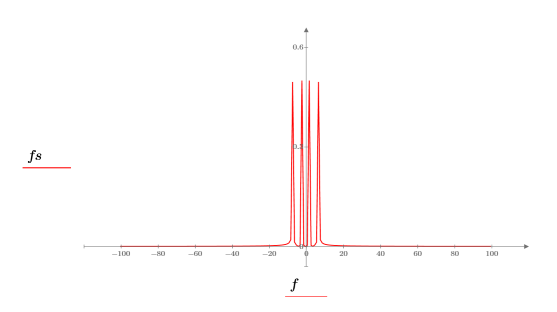
8. Verwenden Sie die Funktionen match und max, um die diskreten Frequenzen zu ermitteln, bei denen die Spitzen auftreten.

<region id="ID0EGPX4" actualWidth="231.2766666666667" actualHeight="36.800000000000004" top="2265.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="297">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="VARIABLE">p2</id>
      <eval>
        <apply>
          <indexer />
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">match</id>
            <sequence>
              <apply>
                <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">max</id>
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">fs</id>
              </apply>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">fs</id>
            </sequence>
          </apply>
          <real>1</real>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EQQX4" actualWidth="556.95384615384614" actualHeight="235.20000000000002" top="2323.2000000000003" left="38.400000000000006" height="235.20000000000002" width="556.95384615384614" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="303">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.953846153846" height="177.6" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-20" end="20">
          <axisLine position="origin" positionticmark="0" legendWidth="59.5966666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="304" display="true" color="#FF0000FF" line-style="Dash" value="1.5">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">f</id>
                <id xml:space="preserve">p2</id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="310">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">f</id>
              </math>
              <math resultRef="311">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="307">
              <real xmlns="http://schemas.mathsoft.com/math50">-20</real>
            </startValue>
            <endValue resultRef="309">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="0.6">
          <axisLine position="origin" positionticmark="5" legendWidth="65.9166666666667" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="312" display="true" color="#FFED1D2F" line-style="DashDotDot" value="0.50020306790574232">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">fs</id>
                <id xml:space="preserve">p2</id>
              </apply>
            </marker>
          </markers>
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="320">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">fs</id>
              </math>
              <math resultRef="321">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="315">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="317">
              <real xmlns="http://schemas.mathsoft.com/math50">0.3</real>
            </secondTickValue>
            <endValue resultRef="319">
              <real xmlns="http://schemas.mathsoft.com/math50">0.6</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

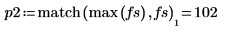
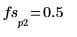
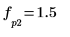
Die enge Beziehung zwischen der Hartley-Transformation und der Fourier-Transformation lässt sich darstellen, indem gezeigt wird, wie Phase und Betrag mit der Hartley-Transformation berechnet werden. Dies kann mithilfe eines kleinen Datensatzes geschehen.

Kurzes und verrauschtes Signal

1. Definieren und plotten Sie ein verrauschtes Eingangssignal mit 7 Abtastpunkten.

<region id="ID0E2TX4" actualWidth="575.84615384615381" actualHeight="312" top="2860.8000000000006" left="38.400000000000006" height="312" width="575.84615384615381" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="339">
          <traceStyle color="#FF0000FF" symbol="filledRectangle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="479.846153846154" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="6">
          <axisLine position="bottom" positionticmark="-1" legendWidth="61.7533333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="340">
                <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">n</id>
              </math>
              <math resultRef="341">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0.21" end="1.09">
          <axisLine position="origin" positionticmark="0" legendWidth="66.5833333333333" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="342">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">v</id>
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
                </apply>
              </math>
              <math resultRef="343">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

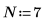
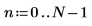
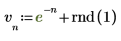
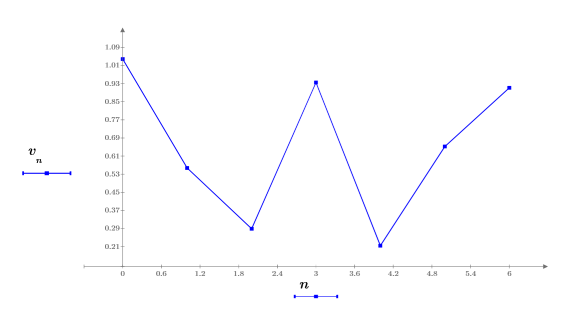
2. Berechnen und zentrieren Sie die diskrete Hartley-Transformation.

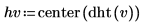
3. Berechnen Sie die ungeraden und geraden Teile der diskreten Hartley-Transformation (diese Formeln setzen einen ungeraden Wert für N voraus).

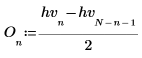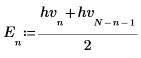4. Verwenden Sie die Funktion angle zur Berechnung des Phasenvektors.

<region id="ID0EI1X4" actualWidth="145.02333333333334" actualHeight="36.800000000000004" top="3475.2000000000007" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="354">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id xml:space="preserve" labels="*">ϕ</id>
        <id xml:space="preserve" labels="*">n</id>
      </apply>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">angle</id>
        <sequence>
          <apply>
            <indexer />
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">E</id>
            <id xml:space="preserve">n</id>
          </apply>
          <apply>
            <neg />
            <apply>
              <indexer />
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">O</id>
              <id xml:space="preserve">n</id>
            </apply>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

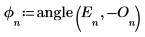
5. Definieren Sie den Betragsvektor.

6. Verwenden Sie die Funktionen phase, phasecor und center, um den Phasenvektor zu erstellen.

<region id="ID0EF5X4" actualWidth="282.13333333333333" actualHeight="25.6" top="3648.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="358">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id xml:space="preserve" labels="*">phs2</id>
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">phasecor</id>
        <apply>
          <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">phase</id>
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">center</id>
            <apply>
              <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">dft</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">v</id>
            </apply>
          </apply>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

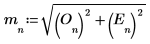
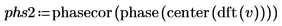
7. Verwenden Sie die Funktion augment, um die Phasenergebnisse mit den Ergebnissen zu vergleichen, die über die Fourier-Transformation ermittelt wurden.

<region id="ID0EHAY4" actualWidth="353.5533333333334" actualHeight="137.2" top="3801.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="360">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">augment</id>
        <sequence>
          <apply>
            <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">phasecor</id>
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">ϕ</id>
          </apply>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">phs2</id>
        </sequence>
      </apply>
      <unitOverride>
        <id xml:space="preserve" labels="*">π</id>
      </unitOverride>
    </eval>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

Die Phasenergebnisse stimmen überein.

8. Verwenden Sie die Funktionen dft und center, um den Betragsvektor zu erstellen.

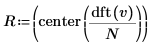
9. Verwenden Sie die Funktion augment, um die Betragsergebnisse mit den Ergebnissen zu vergleichen, die über die Fourier-Transformation ermittelt wurden.

<region id="ID0EXDY4" actualWidth="244.03333333333336" actualHeight="137.2" top="4147.2000000000007" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="364">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION" label-is-contextual="true">augment</id>
        <sequence>
          <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
          <apply>
            <vectorize />
            <apply>
              <absval />
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">R</id>
            </apply>
          </apply>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

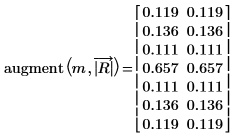
Die Betragsergebnisse stimmen überein.

Eine eingehende Erläuterung der Hartley-Transformation und ihrer Anwendungen finden Sie in Ronald Bracewell, The Hartley Transform (Oxford University Press).

Zugehörige Themen

Hartley-Transformation

So verschieben, löschen oder fügen Sie Markierungen hinzu

War dies hilfreich?