Beispiel: Symbolische Lösungen von Gleichungen
Lösen Sie Gleichungen symbolisch mit einer oder vielen Unbekannten.
Eine einzelne Gleichung lösen
1. Geben Sie die folgende Gleichung ein:
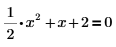
2. Fügen Sie den symbolischen Auswertungsoperator ein, geben Sie das Schlüsselwort solve in den Platzhalter ein, und drücken Sie die EINGABETASTE.
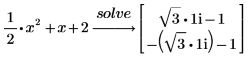
Da die rechte Seite der Gleichung 0 ist, muss der Teil =0 des Ausdrucks nicht eingegeben werden. |
3. Geben Sie die Konstante 2 im Dezimalformat 2.0 ein, um die Antwort im Gleitkomma-Format zurückzugeben.
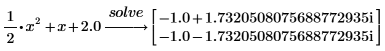
4. Lösen Sie eine Gleichung mit einer Variablen.
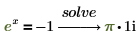
5. Lösen Sie eine Gleichung mit mehreren Variablen.
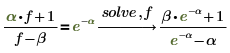
Wenn die Gleichung mehrere Variablen enthält, müssen Sie die Variable festlegen, nach der sie aufgelöst werden soll. |
6. Lösen Sie ein Polynom vierter Ordnung.

Das obige Ergebnis zeigt, dass die symbolische Lösung eines Polynoms vierter Ordnung vier numerische Lösungen ergibt. |
7. Ermitteln Sie die Wurzeln eines Polynoms mit parametrisierten Koeffizienten.
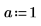
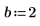
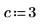
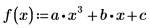
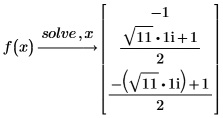
Systeme von Gleichungs- und Gleichheitsbedingungen lösen
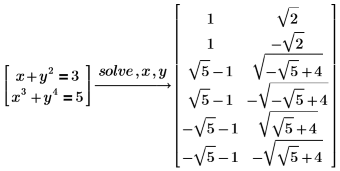
Sie können mehrere Gleichungs- und Gleichheitsbedingungen zusammen als Gleichungssystem auflösen, indem Sie sie in einem Vektor gruppieren.
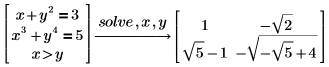
Polynomgleichungen durch Radikale auflösen
Standardmäßig löst PTC Mathcad Polynomgleichungen bis zum vierten Grad durch Radikale auf. Die Lösungen werden unter Verwendung normaler arithmetischer Vorgänge durch Radikale aufgebaut.
1. Lösen Sie das folgende Polynom:
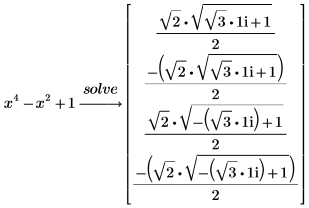
Der Mathematiker Galois bewies im 19. Jahrhundert, dass es Polynome fünften Grades und höher gibt, die nicht durch Radikale aufgelöst werden können. Für diese Polynome gibt PTC Mathcad eine numerische Näherung für die Wurzeln zurück. |
2. Lösen Sie ein Polynom fünften Grades.

Das obige Ergebnis zeigt, dass die symbolische Lösung eines Polynoms fünfter Ordnung fünf numerische Lösungen ergibt. |
Annahmen zum Definitionsbereich einer Variablen aufstellen
Verwenden Sie das Schlüsselwort assume, um Annahmen zum Definitionsbereich einer Variablen im Problem aufzustellen, z.B., dass es sich um eine reelle Zahl handelt.
1. Lösen Sie eine Gleichung unter der Annahme, dass x eine reelle Zahl ist.
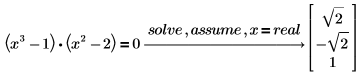
PTC Mathcad gibt nur die reellen Lösungen für die Gleichung zurück. |
2. Verwenden Sie RealRange, um die reellen Lösungen im Bereich (0, 2) zu ermitteln.
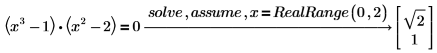
3. Geben Sie x=integer ein, um nur die Ganzzahllösungen zu ermitteln.
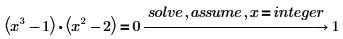
4. Verwenden Sie assume, um den Definitionsbereich einer Variablen in einer symbolischen Auswertung einzuschränken.
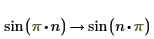
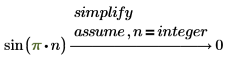
Detaillierte Lösungen für Gleichungen zurückgeben
Fügen Sie den Modifizierer fully nach der Gleichungslösung hinzu, um detaillierte Lösungen für Gleichungen zurückzugeben.
1. Verwenden Sie die Funktion clear.sym, um den vorherigen symbolischen Wert von a zu löschen.
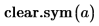
2. Verwenden Sie fully, um die Werte von a zurückzugeben, für die die Lösung gültig ist.
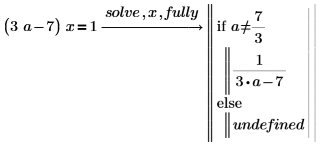
3. Verwenden Sie das detaillierte Ergebnis zum Definieren einer Funktion.
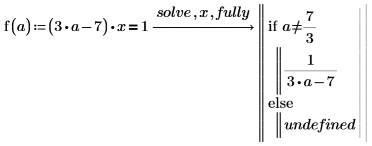
4. Werten Sie die Funktion an a=3 und a=7/3 aus:
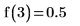
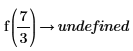
Gleichungen mit periodischen Lösungen
Für Gleichungen mit periodischen Lösungen gibt PTC Mathcad eine einzelne Lösung zurück, gefolgt von einem Ausdruck zum Hinzufügen von ganzzahligen Vielfachen der Periode zur ersten Lösung.
1. Verwenden Sie fully zum Auswerten von sin(x).
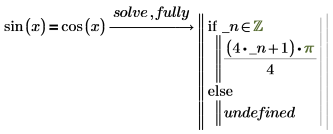
Der Ausdruck, der auf die if-Anweisung folgt, bedeutet pi/4 plus alle ganzzahligen Vielfachen von pi. PTC Mathcad fügt eine neu generierte Variable _n ein, die eine willkürliche Ganzzahl darstellt. Vor der generierten Variable wird ein Unterstrich eingefügt, um Namenskonflikte mit anderen Variablen zu vermeiden, die möglicherweise an anderer Stelle im Arbeitsblatt definiert sind. |
2. Fügen Sie den Modifizierer using hinzu, gefolgt von einer Gleichung mit dem booleschen Operator "gleich", um die generierte Variable mit der neuen Variablen gleichzusetzen.
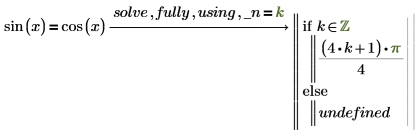
Wenn die nach using angegebene Variable nicht die generierte Variable ist, die von solve zurückgegeben worden ist, gibt PTC Mathcad einen Fehler zurück.