Beispiel: Gleichungslöser für Zustandsräume

Funktionen > Lösen und Optimieren > Lösungsalgorithmen für Differentialgleichungen > Beispiel: Gleichungslöser für Zustandsräume

Verwenden Sie den Gleichungslöser statespace, um eine Zustandsraumdarstellung eines Systems von gewöhnlichen Differentialgleichungen (ODEs) erster Ordnung zu lösen.

Suchen Sie insbesondere die Lösung für den Fall des nicht erzwungenen harmonischen Oszillators, bei dem die rechte Seite der harmonischen Schwingungsgleichung 0 ist:

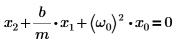
Es gibt vier Fälle für die Lösung – überdämpft, kritisch gedämpft, unterdämpft und vollständige Rückführung.

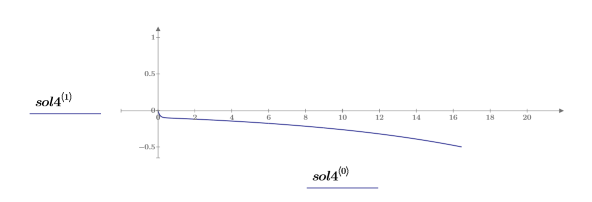
Überdämpfte Lösung

1. Schreiben Sie die mathematische Gleichung für die überdämpfte Lösung:

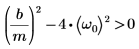
2. Definieren Sie die Anfangsbedingungen, die Masse des Objekts, die Dämpfungskonstante, Start und Ende des Integrationsintervalls sowie die Anzahl der Punkte:

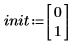
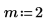
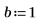
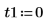
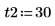
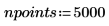
3. Legen Sie die natürliche Frequenz oder Eigenfrequenz des Systems fest.

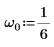
4. Überprüfen Sie, ob die Bedingung der Überdämpfung vorhanden ist:

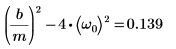
5. Schreiben Sie die GDGL in Matrixform:

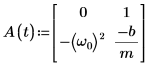
6. Rufen Sie die Funktion statespace auf.

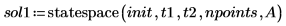
7. Stellen Sie die Lösung grafisch dar:

<region id="ID0ESX25" actualWidth="591.8" actualHeight="288" top="940.80000000000018" left="19.200000000000003" height="288" width="591.8" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="56">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="457.4" height="230.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="33">
          <axisLine position="origin" positionticmark="1" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol1</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol1</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="57">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="58">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

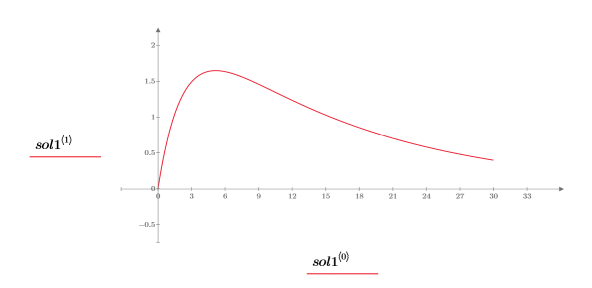
Kritisch gedämpfte Lösung

1. Legen Sie die natürliche Frequenz oder Eigenfrequenz des Systems fest.

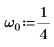
2. Überprüfen Sie, ob die Bedingung der kritischen Dämpfung vorhanden ist:

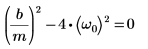
3. Schreiben Sie die GDGL in Matrixform:

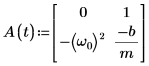
4. Rufen Sie die Funktion statespace auf.

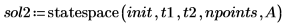
5. Stellen Sie die Lösung grafisch dar:

<region id="ID0ET625" actualWidth="590.8" actualHeight="288" top="1728.0000000000002" left="19.200000000000003" height="288" width="590.8" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="63">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="456.4" height="230.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="33">
          <axisLine position="origin" positionticmark="1" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>12</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol2</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol2</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="64">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="65">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="66">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

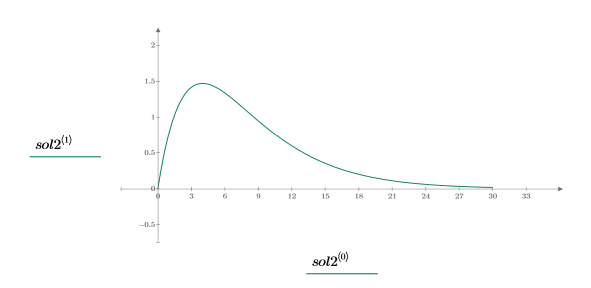
Unterdämpfte Lösung

1. Legen Sie die natürliche Frequenz oder Eigenfrequenz des Systems fest.

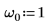
2. Überprüfen Sie, ob die Bedingung der Unterdämpfung vorhanden ist

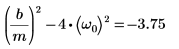
3. Schreiben Sie die GDGL in Matrixform:

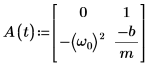
4. Rufen Sie die Funktion statespace auf.

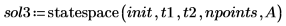
5. Stellen Sie die Lösung grafisch dar:

<region id="ID0EUH35" actualWidth="591.6000126600261" actualHeight="201.60000429153402" top="2592.0000000000005" left="19.200000000000003" height="201.60000429153402" width="591.6000126600261" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="71">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="457.200012660026" height="144.000004291534" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="1" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol3</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="72">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="73">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>4</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol3</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="74">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="75">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="76">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

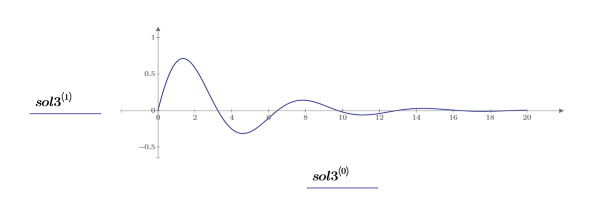
Lösung mit vollständiger Rückführung

1. Legen Sie die Anfangsbedingungen fest.

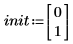
2. Schreiben Sie die GDGL (gewöhnliche Differentialgleichung) in Matrixform.

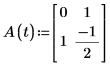
3. Definieren Sie die zusätzlichen Funktionen.

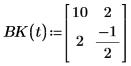
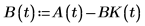
4. Rufen Sie die Funktion statespace auf.

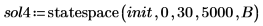
5. Stellen Sie die Lösung grafisch dar.

<region id="ID0EDQ35" actualWidth="591.600012660026" actualHeight="201.60000429153402" top="3801.6000000000004" left="76.800000000000011" height="201.60000429153402" width="591.600012660026" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="82">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="457.200012660026" height="144.000004291534" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="1" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol4</id>
                  <real>0</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="83">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="84">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="89.78" />
          <axisGrid>
            <gridFrequency>4</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <matcol />
                  <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">sol4</id>
                  <real>1</real>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="85">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="86">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="87">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Zugehörige Themen

GDG-Löser für Zustandsräume

War dies hilfreich?