Beispiel: Spektralanalyse
Verwenden Sie die Funktionen coherence, cspectrum, pspectrum und snr, um die Kohärenz, das Kreuzspektrum, das Potenzspektrum und das Signal-Rausch-Verhältnis für ein Signal bzw. Signalpaare zu berechnen.
Eine Beschreibung dieses Mittelwertbildungsverfahrens ist in Signal Processing Algorithms von Samuel Stearns und Ruth David (Prentice-Hall, Inc.) enthalten.
Potenzspektrum – DFT verwenden
Bei langen Zeitreihen, in denen nur wenige Datenpunkte einem Signal entsprechen, ist es wünschenswert, dass das Potenzspektrum die Signalfrequenzen, nicht jedoch Rauschen oder Nullwerte zeigt.
1. Definieren Sie die Fensterbreite.
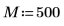
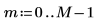
2. Definieren Sie zwei mögliche Fenster, w1 und w2, in denen das Signal nicht null ist.
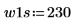 | 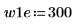 | 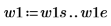 |
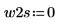 | 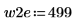 | 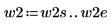 |
3. Legen Sie die Fensterbreite auf eine der beiden möglichen Breiten fest.
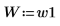
4. Definieren Sie die Signal- und Abtastfrequenzen.
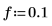
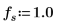
5. Verwenden Sie die Funktion sin, um das Signal innerhalb und außerhalb des ausgewählten Fensters zu definieren.
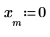
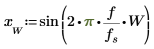
6. Plotten Sie das Signal.
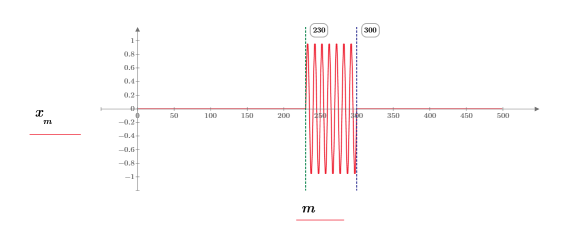
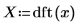
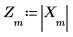
8. Plotten Sie die resultierende Funktion in der Frequenzdomäne.
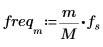
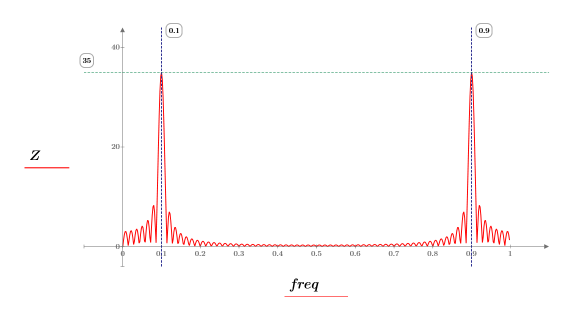
◦ Für ein reines Sinuswellensignal stellt der Betrag der DFT-Koeffizienten eine gute Schätzung seines Potenzspektrums dar. In diesem Fall ist der DFT-Wert des Signals jedoch der Frequenzinhalt des strukturierten Signals, gefaltet mit der Transformation eines rechteckigen Fensters (eine Funktion sinc).
◦ Durch die Einstellung von W= w2 (Schritt 3) wird das Fenster für das Sinuswellensignal von 230 bis 300 auf 0 bis 499 erweitert (um Faktor 7.143x), und dies resultiert in einer Erhöhung des Betrages der beiden Spitzen von 35 auf 250 (ebenfalls um Faktor 7.143x).
◦ Die Frequenzen, bei denen Spitzen auftreten, werden nicht verändert.
Potenzspektrum – pspectrum·verwenden
Die Funktion pspectrum unterteilt die ursprüngliche Zeitreihe in überlappende Segmente. Jedes dieser Segmente wird durch eine DFT transformiert, und die Koeffizienten der transformierten Beträge werden gemittelt. Wenn die Länge der Segmente dieselbe Skalierung hat wie das im Signal zu analysierende Phänomen, dann gibt die Funktion pspectrum eine gute Annäherung des Betrags der Komponenten der interessierenden Teile der ursprünglichen Zeitreihen zurück.
Im Allgemeinen sollte die Länge des Signals mindestens n + 1 betragen.
1. Definieren Sie die Länge des Signals, den Überlappungsbruchteil und den Fenstertyp (konisch-rechteckig).
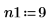 | 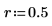 | 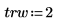 |
2. Verwenden Sie die Funktion pspectrum, um das Potenzspektrum von x zu berechnen, indem Sie x mit dem Überlappungsbruchteil r in n1 überlappende Segmente teilen und jedes Segment mit einem konisch-rechteckigen Fenster darstellen.
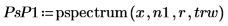
3. Verwenden Sie die Funktionen floor und length, um zu zeigen, dass die Intervalllänge die größte Zahl L ist, für die Folgendes gilt:
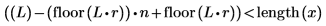
4. Plotten Sie das Spektrum mit einer normalisierten Frequenzachse (1 stellt die Abtastfrequenz dar).
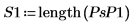
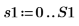
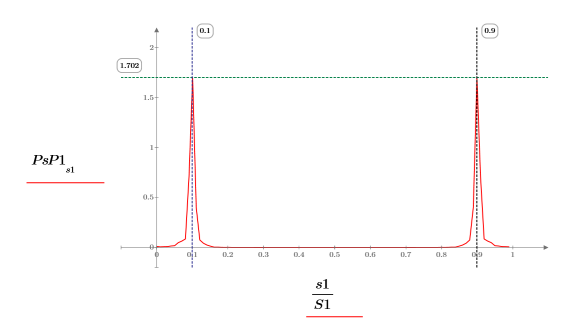
5. Berechnen Sie die durchschnittliche Leistung im Spektrum.
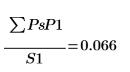
Dies entspricht in etwa dem mittleren Quadratwert von Signal x.
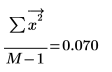
pspectrum mit weißem Rauschen
Berechnen Sie das Potenzspektrum eines Signals, das weißes Rauschen enthält. Generieren Sie zwei Signale dieser Art, das das zweite Signal für Kreuzspektrumberechnungen benötigt wird. Wenden Sie ein Hamming-Fenster auf den Datenblock an, um ihn abzuschrägen.
1. Definieren Sie die Signalbreite.
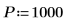
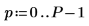
2. Verwenden Sie die Funktionen sin und rnd, um zwei Signale mit einer allgemeinen Frequenz fc zu definieren. Die Funktion rnd gibt einen Vektor gleichförmig verteilter Zufallszahlen zwischen 0 und der angegebenen Zahl zurück und stellt so sicher, dass die Signale unterschiedlich bleiben.
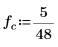
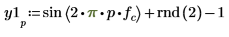
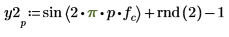
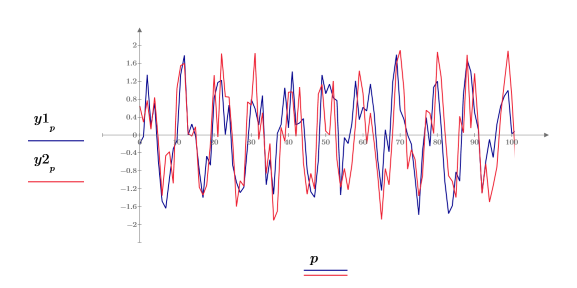
3. Plotten Sie die ersten 100 Samples der beiden Signale.
4. Verwenden Sie die Funktion pspectrum, um das Potenzspektrum von y1 zu erhalten, das berechnet wird, indem Sie es mit einem Überlappungsbruchteil von 0.5 in 40 überlappende Segmente teilen und jedes Segment mit einem Hamming-Fenster darstellen.
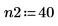 | 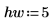 |
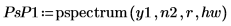 | |
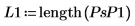 | 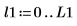 |
5. Verwenden Sie die Funktionen match und max, um die Spitzen-Samples des Leistungsspektrums zu ermitteln.
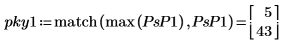
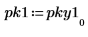
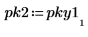
6. Plotten Sie das Spektrum in Dezibel. Verwenden Sie Markierer, um die allgemeine Frequenz und den maximalen Dezibel-Wert zu markieren.
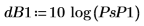
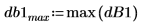
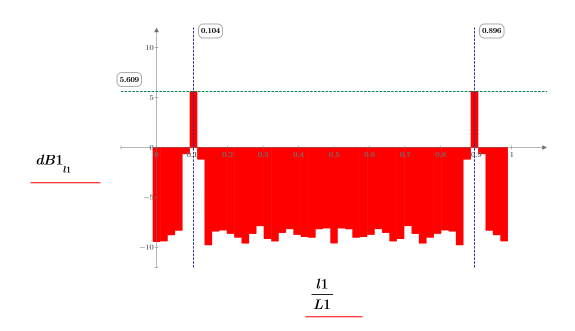
Das Diagramm zeigt, dass die ganze Signalstärke an den allgemeinen Frequenzen fc und 1-fc auftritt.
7. Berechnen Sie die Rauschleistung:
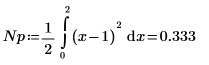
8. Berechnen Sie den Rauschleistungszuwachs in dB.
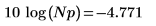
9. Berechnen Sie die Höhe unter Berücksichtigung der Tatsache, dass die Division der beiden obigen Frequenzstichproben durch die Spektrumlänge die durchschnittliche Leistung in der Sinuskomponente ergeben soll, die gleich 0.5 ist.
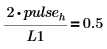 | Oder: | 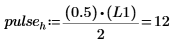 |
10. Vergleichen Sie die theoretischen und tatsächlichen Höhen in Dezibel.
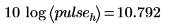
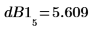
Die Funktion cspectrum
In der Regel wird ein Kreuzspektrum verwendet, um Ähnlichkeiten zwischen zwei Signalen zu erkennen, beispielsweise beim Vergleich einer bekannten Sprachwellenform (z.B. der Vokal 'a') mit einer unbekannten Sprachwellenform (z.B. das Wort 'Apfel'), um festzustellen, ob die bekannte Wellenform in der unbekannten Wellenform enthalten ist. Ebenso wie das Potenzspektrum einer Zeitreihe seiner Autokorrelation ähnelt, ähnelt das Kreuzspektrum von zwei Zeitreihen auch deren Kreuzkorrelation. Für feststehende Zufallsfolgen gibt die Spektrumsfunktion die gleichen Werte wie die Korrelationsfunktion zurück.
1. Wenden Sie die Funktion cspectrum auf die Signale y1 und y2 an. Verwenden Sie dabei 40 überlappende Segmente mit einem Überlappungsbruchteil von 0.5, und stellen Sie jedes Segment mit einem konisch-rechteckigen Fenster dar.
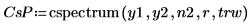
2. Plotten Sie das Spektrum in Dezibel.
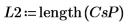 | 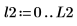 |
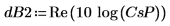 | |
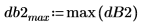 |
3. Plotten Sie das Kreuzspektrum und denken Sie daran, dass es komplex ist. Daher sollte die Logarithmusfunktion auf den Betrag angewendet werden.
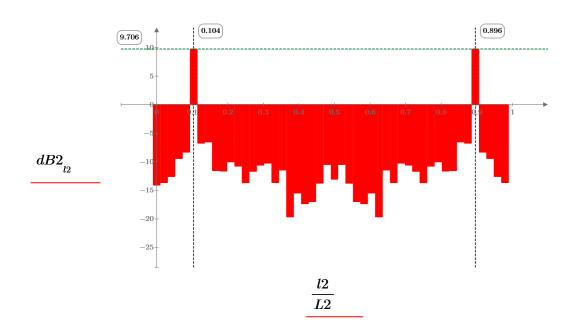
Das Kreuzspektrum von y1 und y2 zeigt einen Spitzenwert an den allgemeinen Frequenzen fc und 1- fc.
Die Funktionen coherence und snr
Die Funktion coherence misst die lineare Abhängigkeit eines Signals von einem anderen und ist gleich der quadrierten Magnitude des Kreuzspektrums zweier Signale geteilt durch beide Potenzspektren. Die Werte bewegen sich im Bereich von 0 bis 1. Werte von 1 für die Funktion coherence geben an, dass beide Signale starke rauschfreie Anteile in dem betreffenden Frequenzband enthalten, während Werte von 0 angeben, dass das Frequenzband überwiegend Rauschen enthält.
Die Funktion snr zur Berechnung des Signal-Rausch-Verhältnisses ist gleich der Kohärenzfunktion geteilt durch (1 minus Funktion "coherence"). Sie wird dort, wo die beiden Signale über starke Komponenten in einem Komponentenband verfügen, proportional zum Verhältnis zwischen der Signalstärke und der Sensorstärke oder der Stärke von Hintergrundgeräuschen maximiert.
1. Wenden Sie die Funktion coherence auf die Signale y1 und y2 an. Verwenden Sie dabei 40 überlappende Segmente mit einem Überlappungsbruchteil von 0.5, und stellen Sie jedes Segment mit einem Hamming-Fenster dar.
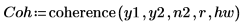 | |
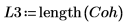 | 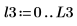 |
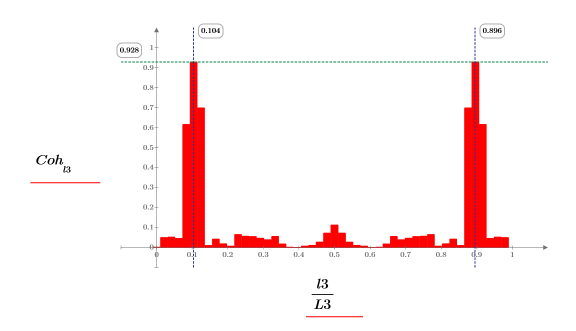
2. Plotten Sie die Funktion "coherence". Verwenden Sie Markierer, um die allgemeine Frequenz und den maximalen Wert zu markieren.
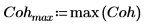
3. Wenden Sie die Funktion snr auf die Signale y1 und y2 an. Verwenden Sie dabei 40 überlappende Segmente mit einem Überlappungsbruchteil von 0.5, und stellen Sie jedes Segment mit einem Hamming-Fenster dar.
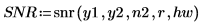 | |
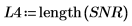 | 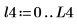 |
4. Plotten Sie die Funktion für das Signal-Rausch-Verhältnis. Verwenden Sie Markierer, um die allgemeine Frequenz und den maximalen Wert zu markieren.
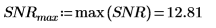
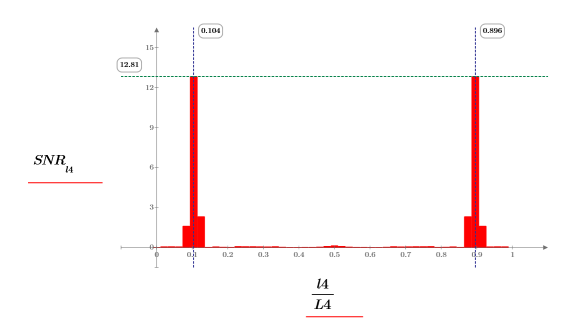
Beide Funktionen coherence und snr zeigen einen maximalen Wert bei den Monofrequenzkomponenten der beiden Signale, wobei zusätzliches Rauschen durch die beiden kleineren Balken links und rechts dargestellt wird.