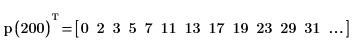Beispiel: Rekursive Funktionen
Definieren Sie mit den PTC Mathcad Programmierfunktionen rekursive Funktionen.
Beispiel 1: Fakultätsfunktion definieren
1. Definieren Sie die Funktion Fac, die die Fakultät von n berechnet. Beschriften Sie die Funktion mit der Beschriftung "Funktion".
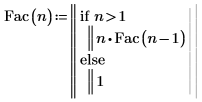
2. Berechnen Sie die Fakultät von 6 mit Fac, und prüfen Sie diese mit dem PTC Mathcad Fakultätsoperator.
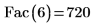
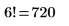
3. Definieren Sie eine weitere Funktion Fac mit einer anderen Bedingung für n, und rufen Sie die Funktion auf, wie unten dargestellt.
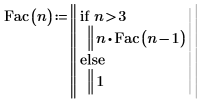
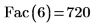
PTC Mathcad berechnet dasselbe Ergebnis, da bei der Berechnung die vorherige Definition von Fac berücksichtigt wird.
4. Deaktivieren Sie die erste Definition von Fac, um den Unterschied in den Ergebnissen zu sehen. Vermeiden Sie diese Unklarheit, indem Sie Funktionsnamen nicht erneut verwenden.
Beispiel 2: Den größten gemeinsamen Teiler zweier positiver Ganzzahlen errechnen
1. Schreiben Sie eine rekursive Funktion GCD zur Berechnung des größten gemeinsamen Teilers von zwei Zahlen. Dies ist die größte Ganzzahl, mit der x und y gleichmäßig geteilt werden.
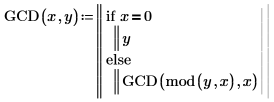
2. Rufen Sie diese Funktion mit verschiedenen Werten auf.
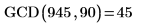 | 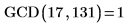 |
Dieses Programm entspricht der integrierten Funktion gcd für den größten gemeinsamen Teiler:
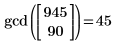 | 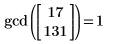 |
Beispiel 3: n-te Iteration einer Funktion f(x) an einem Punkt a definieren
1. Schreiben Sie eine rekursive Funktion "nest" zur Berechnung der n-ten Iteration einer Funktion f(x) an einem Punkt a.
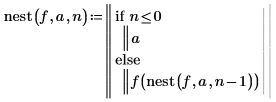
2. Definieren Sie eine Funktion f(x), und weisen Sie a die Zahl 1 zu.
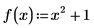
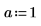
3. Rufen Sie diese Funktion mit verschiedenen Werten auf.
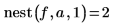 | 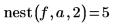 |
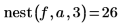 | 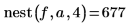 |
Beispiel 4: Fibonacci-Folge definieren (zwei rekursive Aufrufe pro Invocation)
1. Schreiben Sie eine Funktion fib zur Berechnung des Wertes der Fibonacci-Folge für n.
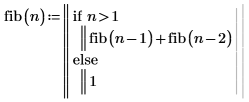
2. Definieren Sie einen Vektor k, und rufen Sie die Funktion fib auf.
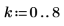

Beispiel 5: Partitionsfunktion definieren
1. Schreiben Sie eine rekursive Funktion part zur Berechnung der verschiedenen Möglichkeiten, die es gibt, um m als Summe positiver Ganzzahlen auszudrücken, ohne n zu überschreiten.

2. Rufen Sie die Funktion mit verschiedenen Werten auf.
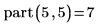
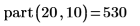
Beispiel 6: Zufällige Binärstruktur erstellen
1. Schreiben Sie eine rekursive Funktion Tree zum Erstellen einer zufälligen Binärstruktur.
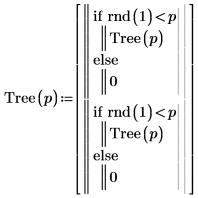
2. Rufen Sie die Funktion auf.

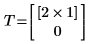
Beispiel 7: Höhe einer Binärstruktur ermitteln
1. Schreiben Sie eine rekursive Funktion height zur Rückgabe der Höhe einer Binärstruktur.
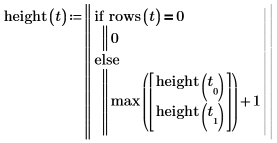
2. Rufen Sie die Funktion mit der im vorherigen Beispiel erstellten Struktur auf.
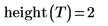
Da Tree einen zufälligen Binärbaum erstellt, ändert sich die zurückgegebene Höhe nach jeder Neuberechnung. |
Beispiel 8: Sieb des Eratosthenes zur Ermittlung von Primzahlen einrichten
1. Verwenden Sie die Funktion ceil, um eine rekursive Funktion p zu schreiben, die alle Primzahlen kleiner als n, unter Verwendung des Siebs des Eratosthenes, berechnet.

2. Rufen Sie die Funktion auf, um einen Vektor aller Primzahlen unter 200 zu erhalten.