Beispiel: Wahrscheinlichkeitsdichte und kumulative Wahrscheinlichkeitsverteilung

Funktionen > Statistik > Wahrscheinlichkeitsverteilungen > Beispiel: Wahrscheinlichkeitsdichte und kumulative Wahrscheinlichkeitsverteilung

Demonstrieren Sie mit den Funktionen dnorm, pnorm, cnorm und qnorm die Unterschiede zwischen verschiedenen Wahrscheinlichkeitsfunktionen.

1. Definieren Sie den Mittelwert und die Standardabweichung einer Normalverteilung.

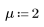
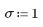
2. Plotten Sie die Wahrscheinlichkeitsdichte (blau) und die kumulative Wahrscheinlichkeit (schwarz und rot) von Normalverteilungen.

<region id="ID0E13SBB" top="144" left="24" width="525" height="219" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace num-of-points="500">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace num-of-points="500">
          <traceStyle color="#FF000000" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace num-of-points="500">
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <real xmlns="http://schemas.mathsoft.com/math50">-4</real>
            </startValue>
            <endValue>
              <real xmlns="http://schemas.mathsoft.com/math50">6</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="4" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id>dnorm</id>
                  <sequence>
                    <id>x</id>
                    <id>μ</id>
                    <id>σ</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id>pnorm</id>
                  <sequence>
                    <id>x</id>
                    <id>μ</id>
                    <id>σ</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id>cnorm</id>
                  <id>x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

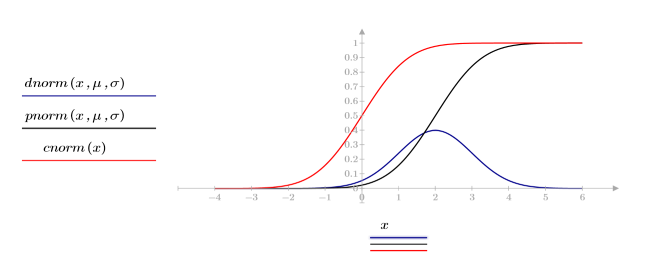
Die Funktion dnorm berechnet die Wahrscheinlichkeitsdichte bei x einer Normalverteilung mit dem Mittelwert μ und der Standardabweichung σ. Die Funktion pnorm berechnet die kumulative Wahrscheinlichkeitsverteilung der Normalverteilung. Die Funktion cnorm steht für die kumulative Wahrscheinlichkeitsverteilung der Normalverteilung, wobei μ = 0 und σ = 1.

3. Verwenden Sie die Funktion qnorm, um den Wert von x zu berechnen, wenn die Fläche unter der Kurve von - ∞ bisx der halben Fläche unter der gesamten Kurve entspricht.

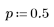
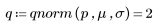
In diesem Fall ist der Wert von x gleich dem Mittelwert. Dies wird durch folgende Formel bestätigt:

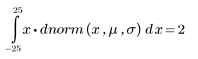
Die Wahrscheinlichkeitsdichte bei q lässt sich mühelos mithilfe der Funktion pnorm ausfindig machen. Diese Funktion ist die Umkehrfunktion von qnorm:

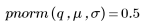
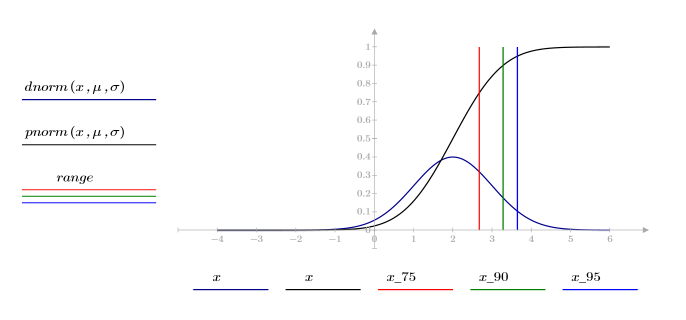
4. Ermitteln Sie mithilfe der Funktion qnorm das 75., 90. und 95. Perzentil der Normalverteilung.

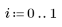
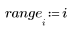
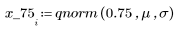
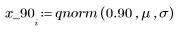
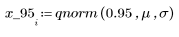
5. Plotten Sie die Wahrscheinlichkeitsdichte (blau) und die kumulative Wahrscheinlichkeitsverteilung (schwarz) einer Normalverteilung, und fügen Sie die oben berechneten Perzentile (75 %: rot, 90 %: grün, 95 %: blau) hinzu.

<region id="ID0E2GTBB" top="1128" left="24" width="549" height="256" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace num-of-points="500">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace num-of-points="500">
          <traceStyle color="#FF000000" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FFFF0000" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF008000" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace>
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <axes>
        <xAxis legend-position="PlotBoundaryBottom" rank="1">
          <axisLine position="origin" positionticmark="0" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">x_75</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">x_90</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">x_95</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <real xmlns="http://schemas.mathsoft.com/math50">-4</real>
            </startValue>
            <secondTickValue>
              <real xmlns="http://schemas.mathsoft.com/math50">-3</real>
            </secondTickValue>
            <endValue>
              <real xmlns="http://schemas.mathsoft.com/math50">6</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis legend-position="PlotBoundaryLeft" rank="1">
          <axisLine position="origin" positionticmark="4" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id>dnorm</id>
                  <sequence>
                    <id>x</id>
                    <id>μ</id>
                    <id>σ</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id>pnorm</id>
                  <sequence>
                    <id>x</id>
                    <id>μ</id>
                    <id>σ</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <id xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Zugehörige Themen

Normalverteilung

War dies hilfreich?