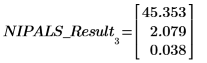Beispiel: Hauptkomponentenanalyse 1
Führen Sie mithilfe der Funktionen Nipals, loadings, scores, PCAeigenvals und PCAvariance eine Hauptkomponentenanalyse durch.
Funktion Nipals
1. Definieren Sie einen Datensatz, in dem jede Spalte für eine Variable steht.


2. Plotten Sie den Datensatz.
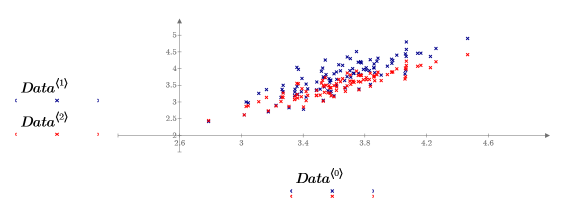
In diesem Graphen überlagern sich die x-y-Ebene und die x-z-Ebene, damit der Datentrend erkennbar wird. Die Daten bilden in der Tat eine elliptische Punktwolke, die fast auf einer Ebene liegt. Zwischen den drei Variablen besteht eine lineare Beziehung und die Abweichung von einer perfekten Ebene ist durch Rauschen bedingt.
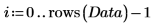
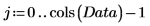
4. Verwenden Sie die Funktion mean, um den Mittelwert der Daten zu ermitteln, und subtrahieren Sie ihn anschließend von jeder Variable, um die Daten zu zentrieren.
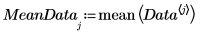
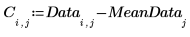
5. Plotten Sie die zentrierten Daten.
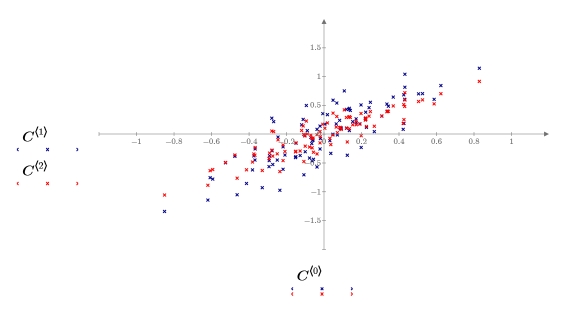
• Die Daten werden jetzt um den Ursprung zentriert. Dies ist einer der Schritte, den die Funktion Nipals automatisch ausführt. • In vielen PCA-Anwendungen ist es zudem wünschenswert, die Daten so zu skalieren, dass die Variablen die gleiche Gewichtung haben, z.B. wenn verschiedene Variablen in unterschiedlichen Einheiten angegeben werden. Es ist zwar gängig, jede Variable (jede Spalte von Data) auf die Einheitenvarianz zu skalieren, in diesem Fall ist dies jedoch nicht angemessen, und daher wird hier nicht skaliert. |
6. Verwenden Sie die Funktion Nipals, um einen neuen variablen Raum zu erstellen. Verwenden Sie drei Hauptkomponenten. Dies ist die größtmögliche Anzahl, da nur drei Variablen zur Verfügung stehen.
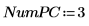
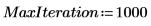
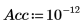
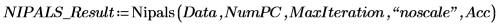
Die Funktion Nipals gibt eine geschachtelte Matrix aus, die aus sechs einzelnen Matrizen besteht. Verwenden Sie sie, um loadings, scores, eigenvals und eigenvecs für die Daten zu ermitteln. Verwenden Sie bei Bedarf die Funktion Nipals2 und die letzten beiden Matrizen, um zusätzliche Komponenten zu extrahieren.
Ladungen und Ergebnisse
1. Rufen Sie die Funktion loadings auf, um die Daten abzurufen, die in der zweiten Matrix von NIPALS_Result enthalten sind.
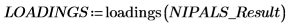
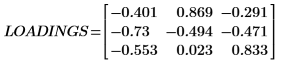
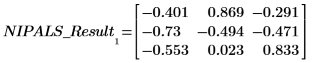
Jede Spalte von LOADINGS ist ein Ladungsvektor.
2. Rufen Sie die Funktion scores auf, um die Daten abzurufen, die in der ersten Matrix von NIPALS_Result enthalten sind.
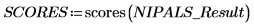

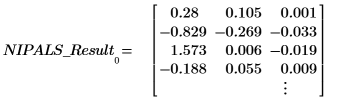
Die Punkte stellen die Größenverhältnisse dar, in denen die Ladungsvektoren hinzugefügt werden, um das ursprüngliche Spektrum nachzubilden. Stellen können Sie sich als Intensitäten vorstellen. Daten = LOADINGS * SCOREST.
3. Stellen Sie die in der Matrix SCORES gespeicherten Daten grafisch dar.
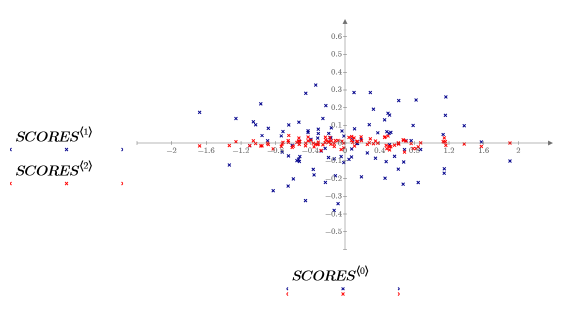
Die Daten wurden gedreht, so dass der maximale Varianzbetrag durch die erste Variable erklärt werden kann. Dies wird im Graphen durch die lange Achse der elliptischen Wolke dargestellt, die jetzt parallel zur x-Achse verläuft. Die Werte für die dritte Variable, die parallel zur z-Achse ist, sind sehr klein. Diese Variable kann in den meisten Fällen vernachlässigt werden. Sie haben die Daten komprimiert.
PCA-Varianz und Eigenwerte
1. Verwenden Sie die Funktion PCAvariance, um die kumulierten Varianzen der drei Hauptkomponenten zurückzugeben.
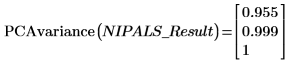
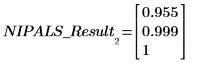
Die ersten beiden Komponenten sind für 99.9 % der Varianz des Systems verantwortlich.
2. Extrahieren Sie mithilfe der Funktion PCAeigenvals die Eigenwerte der Hauptkomponenten.