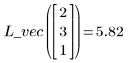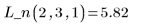Beispiel: Stückweise quadratische Anpassung
Univariate Polynomregression
Verwenden Sie die Funktion loess, um eine Reihe quadratischer Funktionen unter Verwendung der lokalen Regression an Daten anzupassen.
1. Definieren Sie die folgende Matrix:

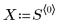
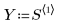
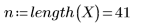
2. Definieren Sie den Bereich oder den Prozentanteil der Gesamtanzahl von Punkten in einem gewichteten Fenster um jeden Datenpunkt, der von der Funktion loess für sukzessive quadratische Anpassungen verwendet wird.
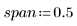
Als allgemeine Richtlinie gilt, dass (span*n) > 1 sein sollte, da der Durchschnitt der Anzahl von Punkten, die größer als 1 sind, in jede gewichtete Kleinste-Quadrate-Anpassung einbezogen werden soll:
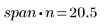
3. Rufen Sie die Funktionen loess und interp auf, um die stückweise quadratische Anpassung durchzuführen.
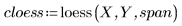
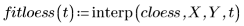
4. Rufen Sie die Funktion polyfit auf, um ein Polynom zweiten Grades an den Datensatz anzupassen.
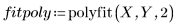
5. Stellen Sie die beiden oben definierten Kurven grafisch dar.
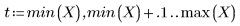
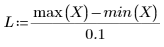
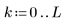
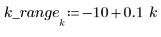
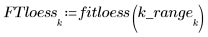
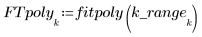
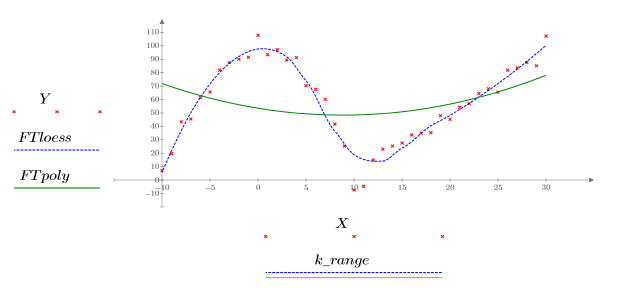
• Wenn der Bereich groß ist (beispielsweise 2 oder 3), werden die Daten als eine quadratische Anpassung mit fast gleicher Gewichtung betrachtet. Die Anpassung nähert sich der Lösung polyfit bis zu einem quadratischen Polynom.
• Es gibt keine genauen Richtlinien für die Auswahl des Bereichs. Je größer der Bereich desto glatter wird das Diagramm der Anpassung loess, weil darin weniger Elemente verbunden werden. Die Anpassung bildet jedoch möglicherweise Dateneigenschaften nicht korrekt ab. Wenn der Bereich dagegen zu klein wird, konvergiert loess unter Umständen nicht.
• Der Algorithmus loess ist nicht für die Extrapolation vorgesehen. Wenn Sie versuchen, interp für Werte auszuwerten, die über den ursprünglichen x-Bereich hinausgehen, wird ein Fehler zurückgegeben.
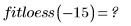
• Sie sollten loess verwenden, wenn die Daten nicht ganz stetig sind, Sie aber keine manuelle stückweise Anpassung vornehmen oder komplexe, physisch unrealistische oder nichtlineare Anpassungsmethoden einsetzen möchten.
Multivariate Polynomregression
Führen Sie mithilfe der Funktion loess eine multivariate Polynomregression durch. Die Funktion loess kann nicht mehr als vier unabhängige Variablen einpassen.
1. Definieren Sie einen Datensatz.
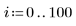
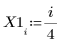
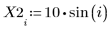
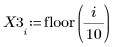
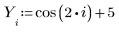
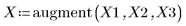
2. Definieren Sie einen Glättungsparameter.
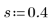
Der Parameter hat die gleiche Bedeutung wie im Fall mit einem Faktor.
3. Rufen Sie die Funktion loess auf.
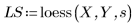
4. Rufen Sie die Funktion interp auf, um die multivariate Anpassungsfunktionen zu interpolieren. Die Anpassungsfunktion kann entweder einen Vektor von n Elementen oder einen Satz von n Argumenten verarbeiten, wobei n für die Anzahl von unabhängigen Faktoren steht.
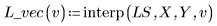
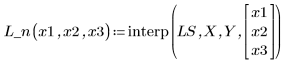
5. Verwenden Sie die Anpassungsfunktionen, um den Wert von Y am Punkt (2, 3, 1) vorherzusagen.