Beispiel: Momentinvarianten
Berechnen Sie mithilfe der Funktion moment_invariant die sieben invarianten, räumlichen Momente für ein Bild.
Invariante Momente sind Merkmale eines Bildes, die sich bei einer Translation, Rotation oder Skalierung des Bildes nicht verändern. Sie sind bei Mustererkennungsproblemen sehr hilfreich.
Weitere Informationen zur Verwendung dieses Beispiels finden Sie unter Bildverarbeitungsbeispiele.
Einfaches Bild
1. Definieren Sie eine einfache Bildmatrix, und verwenden Sie anschließend die Funktion WRITEBMP, um das Bild in einer Datei zu speichern.
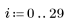
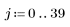
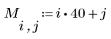
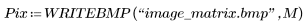

(image_matrix.bmp)
2. Berechnen Sie die Momente bis zum zweiten Grad bzw. Bildschwerpunkt.
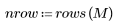
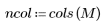
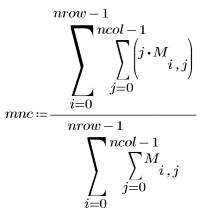
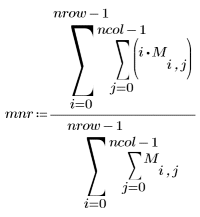
3. Berechnen Sie die zentralen Momente bis zum dritten Grad.
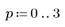
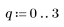
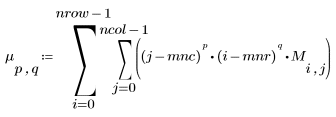

4. Berechnen Sie die normalisierten Momente.
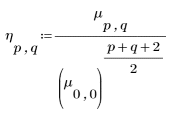
5. Berechnen Sie die erste Momentinvariante.
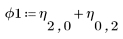
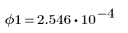
6. Rufen Sie die Funktion moment_invariant auf und vergleichen Sie die Ergebnisse.
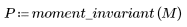
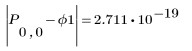
Geometrische Transformationen
1. Verwenden Sie die Funktion READ_IMAGE, um ein Bild einzulesen.
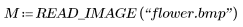

(flower.bmp)
2. Verwenden Sie die Funktionen translate, rotate und zoom, um die folgenden 3 geometrischen Transformationen am Bild durchzuführen: Translation, Rotation und Skalierung.
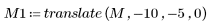 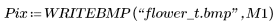 |  (flower_t.bmp) |
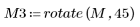 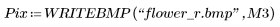 |  (flower_r.bmp) |
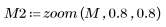 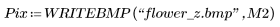 |  (flower_z.bmp) |
3. Wenden Sie moment_invariant auf das Bild an und berechnen Sie die Ergebnisse.
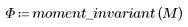
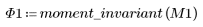
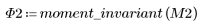
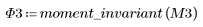
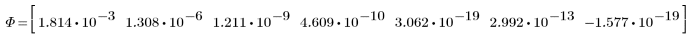
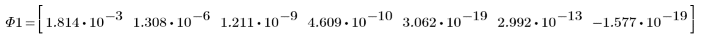
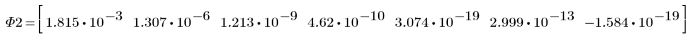
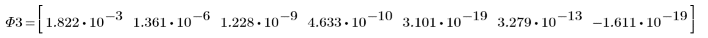
Die invarianten Momente werden nicht verändert.
Zwischen den obigen Ergebnissen und den Invarianten, die für das Originalbild berechnet wurden, besteht eine annehmbare Übereinstimmung. Die kleinen Fehler gehen auf das Auffüllen mit Nullen und die Pixelinterpolation zurück, die in den Transformationen ausgeführt wird.
4. Ändern Sie die Transformationswerte und vergleichen Sie die Momentinvarianten mit den ursprünglichen Momentinvarianten.
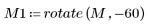
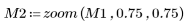
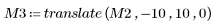
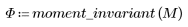
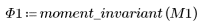
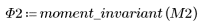
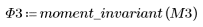
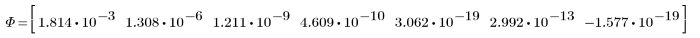
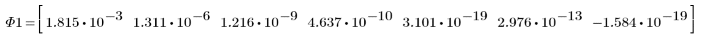
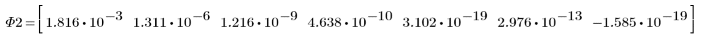
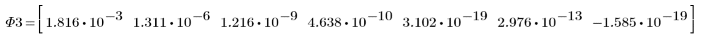
Zwischen den obigen Ergebnissen und den Invarianten, die für das Originalbild berechnet wurden, besteht ebenfalls eine annehmbare Übereinstimmung.