Beispiel: LU-Matrixfaktorisierung

Funktionen > Vektor und Matrix > Matrixfaktorisierung > Beispiel: LU-Matrixfaktorisierung

Beispiel: LU-Matrixfaktorisierung

Verwenden Sie die Funktion LU, um eine LU-Matrixfaktorisierung auszuführen.

Um logische Konflikte zu vermeiden, wenn Sie boolesche Vergleiche ausführen, aktivieren Sie Annähernde Gleichheit in der Dropdown-Liste Berechnungsoptionen.

LU-Faktorisierung einer reellen Matrix

1. Definieren Sie eine reelle Matrix M1 mit den Dimensionen m x n, wobei gilt: m > n.

Zum Kopieren dieses Ausdrucks klicken

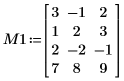
2. Verwenden Sie die Funktion LU, um eine LU-Matrixfaktorisierung der Matrix M1 durchzuführen.

Zum Kopieren dieses Ausdrucks klicken

3. Zeigen Sie, dass P1 x M1 = L1 x U1.

<region id="ID0EPANFB" actualWidth="165.19" actualHeight="81.4" top="614.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="83"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P1</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m1</id> <real>0</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> </math> </region>	<region id="ID0E6ANFB" actualWidth="255.11666666666667" actualHeight="81.4" top="710.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="85"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L1</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m1</id> <real>1</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true"> <nestedMatrixFormats> <nestedMatrixFormat size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" position="0,0" /> </nestedMatrixFormats> </matrix> </resultFormat> </math> </region>	<region id="ID0EPBNFB" actualWidth="228.27" actualHeight="62.800000000000004" top="787.20000000000016" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="87"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">U1</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m1</id> <real>2</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true"> <nestedMatrixFormats> <nestedMatrixFormat size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" position="0,0" /> </nestedMatrixFormats> </matrix> </resultFormat> </math> </region>
<region id="ID0EDCNFB" actualWidth="158.74333333333334" actualHeight="81.4" top="921.60000000000014" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="89"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>	<region id="ID0ETCNFB" actualWidth="154.49" actualHeight="81.4" top="921.60000000000014" left="211.20000000000005" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="91"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U1</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>
<region id="ID0EPDNFB" actualWidth="151.08" actualHeight="25.6" top="998.40000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="93"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U1</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </math> </region>

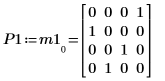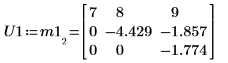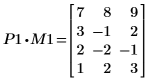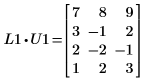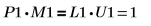Die Beziehung ist logisch wahr.

4. Verwenden Sie die Funktion submatrix, um die Matrix M2 zu extrahieren, wobei Folgendes gilt: m < n.

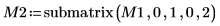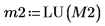5. Zeigen Sie, dass P2 x M2 = L2 x U2.

<region id="ID0EWKNFB" actualWidth="69.890000000000015" actualHeight="36.800000000000004" top="1228.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="99"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>0</real> </apply> </define> </math> </region>	<region id="ID0EELNFB" actualWidth="69.276666666666671" actualHeight="36.800000000000004" top="1228.8000000000002" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="101"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>1</real> </apply> </define> </math> </region>	<region id="ID0ESLNFB" actualWidth="70.77000000000001" actualHeight="36.800000000000004" top="1228.8000000000002" left="230.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="103"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">U2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>2</real> </apply> </define> </math> </region>
<region id="ID0EFMNFB" actualWidth="151.08" actualHeight="25.6" top="1267.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="105"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P2</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M2</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L2</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U2</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

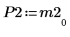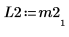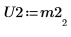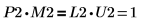Die Beziehung ist logisch wahr.

6. Verwenden Sie die Funktion submatrix, um die Matrix M3 zu extrahieren, wobei Folgendes gilt: m = n.

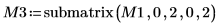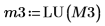7. Zeigen Sie, dass P3 x M3 = L3 x U3.

<region id="ID0EZSNFB" actualWidth="69.890000000000015" actualHeight="36.800000000000004" top="1497.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="111"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EJTNFB" actualWidth="69.276666666666671" actualHeight="36.800000000000004" top="1497.6000000000001" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="113"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EZTNFB" actualWidth="70.77000000000001" actualHeight="36.800000000000004" top="1497.6000000000001" left="230.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="115"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">U3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>2</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0ENUNFB" actualWidth="151.08" actualHeight="25.6" top="1536.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="117"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P3</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M3</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L3</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U3</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

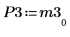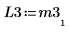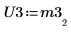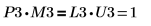Die Beziehung ist logisch wahr.

LU-Faktorisierung einer komplexen Matrix

1. Definieren Sie eine komplexe Matrix C1 mit den Dimensionen m x n, wobei gilt: m > n.

Zum Kopieren dieses Ausdrucks klicken

<region id="ID0EMXNFB" actualWidth="169.16" actualHeight="81.4" top="1708.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="119">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">C1</id>
      <matrix rows="4" cols="3">
        <real>3</real>
        <apply>
          <minus />
          <real>1</real>
          <imag symbol="i">3</imag>
        </apply>
        <apply>
          <minus />
          <imag symbol="i">2</imag>
          <real>3</real>
        </apply>
        <real>7</real>
        <imag symbol="i">-1</imag>
        <real>2</real>
        <real>-2</real>
        <real>8</real>
        <real>2</real>
        <real>3</real>
        <real>-1</real>
        <apply>
          <plus />
          <imag symbol="i">9</imag>
          <real>1</real>
        </apply>
      </matrix>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

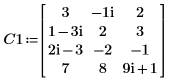
2. Verwenden Sie die Funktion LU, um eine LU-Matrixfaktorisierung der Matrix C1 durchzuführen.

Zum Kopieren dieses Ausdrucks klicken

3. Zeigen Sie, dass P4 x C1 = L4 x U4.

<region id="ID0EA3NFB" actualWidth="158.44333333333333" actualHeight="81.4" top="2073.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="123"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P4</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c1</id> <real>0</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EQ3NFB" actualWidth="425.96999999999997" actualHeight="81.4" top="2169.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="125"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L4</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c1</id> <real>1</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true"> <nestedMatrixFormats> <nestedMatrixFormat size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" position="0,0" /> </nestedMatrixFormats> </matrix> </resultFormat> </math> </region>	<region id="ID0EA4NFB" actualWidth="293.66666666666663" actualHeight="62.800000000000004" top="2246.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="127"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">U4</id> <eval> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c1</id> <real>2</real> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true"> <nestedMatrixFormats> <nestedMatrixFormat size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="true" position="0,0" /> </nestedMatrixFormats> </matrix> </resultFormat> </math> </region>
<region id="ID0EU4NFB" actualWidth="225.19000000000003" actualHeight="81.4" top="2323.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="129"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P4</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">C1</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EE5NFB" actualWidth="224.34000000000003" actualHeight="81.4" top="2323.2000000000003" left="268.80000000000007" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="131"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L4</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U4</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" /> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EA6NFB" actualWidth="147.67666666666668" actualHeight="25.6" top="2380.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="133"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P4</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">C1</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L4</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U4</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

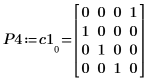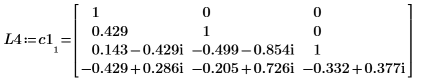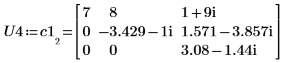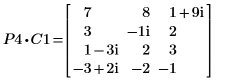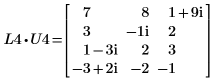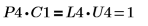Die Beziehung ist logisch wahr.

4. Verwenden Sie die Funktion submatrix, um die Matrix C2 zu extrahieren, wobei Folgendes gilt: m < n.

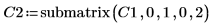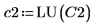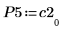5. Zeigen Sie, dass P5 x C2 = L5 x U5.

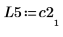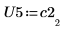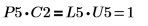Die Beziehung ist logisch wahr.

6. Verwenden Sie die Funktion submatrix, um die Matrix C3 zu extrahieren, wobei Folgendes gilt: m = n.

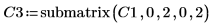
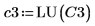
7. Zeigen Sie, dass P6 x C3 = L6 x U6.

<region id="ID0E3MOFB" actualWidth="63.143333333333345" actualHeight="36.800000000000004" top="2880.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="151"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P6</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c3</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EMNOFB" actualWidth="62.53" actualHeight="36.800000000000004" top="2880.0000000000005" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="153"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">L6</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c3</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0E3NOFB" actualWidth="64.023333333333341" actualHeight="36.800000000000004" top="2880.0000000000005" left="230.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="155"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">U6</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">c3</id> <real>2</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EQOOFB" actualWidth="147.67666666666668" actualHeight="25.6" top="2918.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="157"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P6</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">C3</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">L6</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">U6</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>

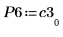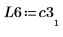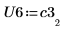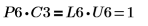Die Beziehung ist logisch wahr.

Zugehörige Themen

Matrixfaktorisierungsfunktionen

War dies hilfreich?