Beispiel: Methoden der linearen Extrapolation
Erzeugen Sie mithilfe der Funktionen burg und yulew Koeffizienten für das benannte lineare Vorhersagemodell. Diese Funktionen implementieren die Burg-Methode beziehungsweise den Yule-Walker-Algorithmus. Eine Beschreibung dieser Algorithmen und der zugrunde liegenden Mathematik finden Sie in Sophocles J. Orfanidis, Optimum Signal Processing, Macmillan (1989).
Yule-Walker-Vorhersage
1. Verwenden Sie die Funktion cos, um ein Kosinussignal zu definieren.
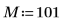
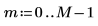
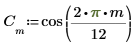
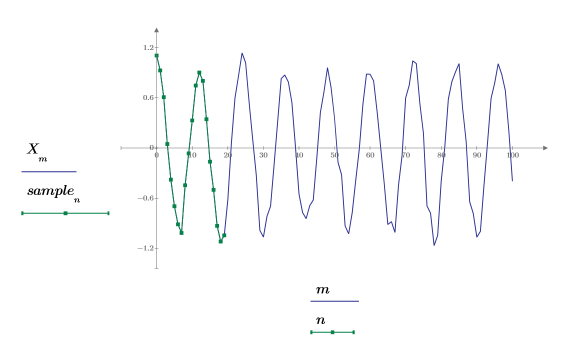
2. Plotten Sie das Signal.
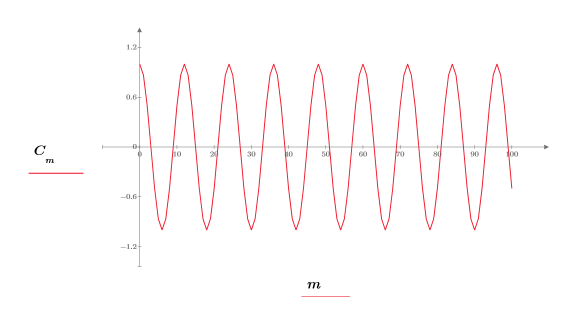
3. Fügen Sie dem Signal mit der Funktion rnd Zufallsrauschen hinzu.
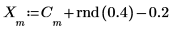
4. Plotten Sie das ursprüngliche Signal und das Signal mit dem Rauschen.
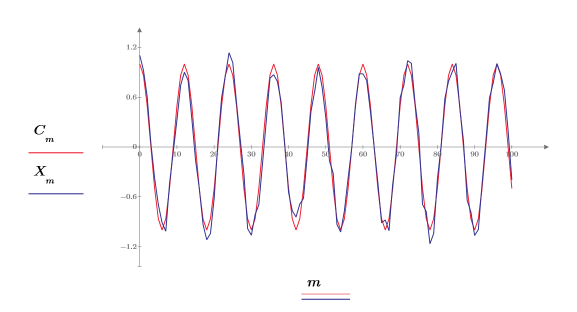
0.2 wird vom Signal subtrahiert, um die Zufallskomponente um die 0-Amplitude zu zentrieren.
5. Nehmen Sie eine kurze Stichprobenmenge vom Anfang des Signals.
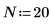
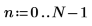
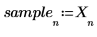
6. Legen Sie die Vorhersagereihenfolge fest, und berechnen Sie mit der Funktion yulew die Koeffizienten.
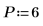
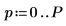

◦ Diese Koeffizienten sind für einen All-Pole-Filter vorgesehen, der das ursprüngliche Signal approximiert. Wie erwartet, gibt es einen großen Pol, der den Kosinus darstellt, und mehrere kleinere Pole, die Näherungen des Rauschens bilden.
◦ Die Reihenfolge P bestimmt die Anzahl aufeinanderfolgender Werte, die zum Vorhersagen des nächsten Werts in der Sequenz verwendet wird. Die ersten sechs Elemente des Koeffizientenvektors werden verwendet, wobei das nullte Elemente ignoriert wird, das stets gleich 1 ist. Diese 1 wird benötigt, wenn y als Vorhersagefehlerfilter verwendet wird, um einen vollständigen Satz von Vorhersagefehlern zu generieren.
7. Vergleichen Sie die vorhergesagten Punkte, die mithilfe der vorherigen P-Punkte im Signal berechnet wurden, mit den Originaldaten. Dies zeigt, wie gut der Filter wäre, wenn er statt des Signals X verwendet würde.
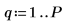
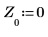
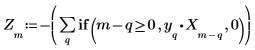
8. Plotten Sie das ursprüngliche und das vorhergesagte Signal.
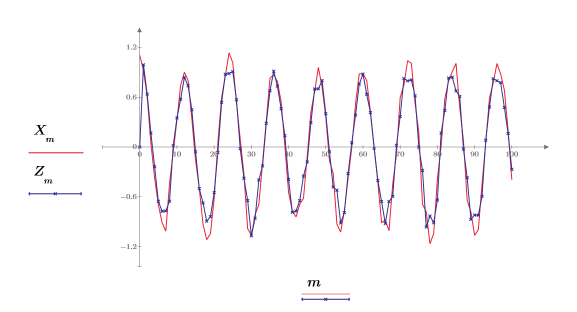
Die Näherung ist sehr gut, sogar wenn nur die ersten 20 Datenpunkte verwendet werden.
9. Generieren Sie mit der Funktion response die Vorhersagefehler für den Yule-Walker-Koeffizienten, indem Sie das Koeffizienten-Array als Filter verwenden und dann die Antwort berechnen, wobei Sie die Stichprobe als Eingabe nutzen.
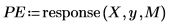
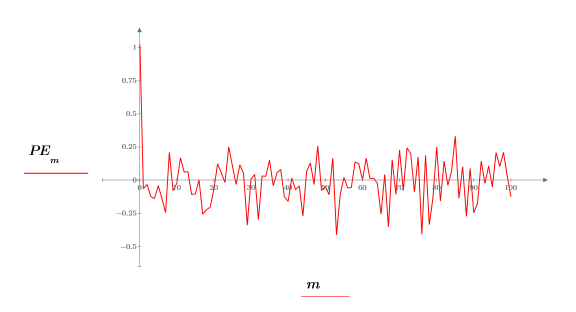
Das vollständige Koeffizienten-Array wird gelegentlich auch Vorhersagefehlerfilter genannt.
10. Verifizieren Sie, dass diese Fehler den Unterschied zwischen den beiden vorherigen Diagrammen erklären.
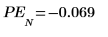
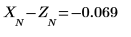
Der Yule-Walker-Algorithmus minimiert die Summe der Quadrate der Vorhersagefehler.
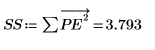
11. Überprüfen Sie die Minimierung stichprobenhaft, indem Sie y stören (indem Sie allen Koeffizienten außer dem ersten einen kleinen, zufällig gewählten Betrag hinzufügen) und die Summe neu berechnen (indem Sie mit dem Cursor auf die Funktion rnd unten zeigen und einige Male die Taste [F5] drücken).
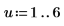
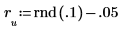
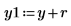
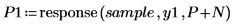
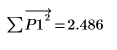
Burg-Vorhersage
1. Erstellen Sie eine Sequenz, für die sich das lineare Vorhersageverfahren gut eignen sollte: einen autoregressiven Prozess mit bekannten Koeffizienten.
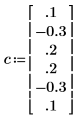
2. Initialisieren Sie die Zeitreihen.
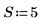
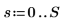
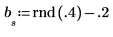
3. Generieren Sie die restlichen Reihen mithilfe von Autoregression und Rauschen.
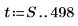
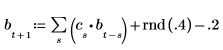
4. Nehmen Sie gesamte Zeitreihe als Stichprobe, berechnen Sie Koeffizienten für ein Modell der 6. Ordnung, und verwenden Sie dann die Funktion burg, um die Koeffizienten zu berechnen.
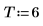
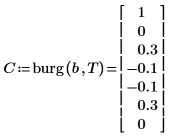
5. Vergleichen Sie die Koeffizienten, mit denen der Prozess tatsächlich generiert wurde, mit der Vorzeichenkonvention dieses Dokuments.
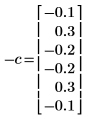
◦ Der nullte Koeffizient wurde ausgelassen, da er immer gleich 1 ist.
◦ Die berechneten Elemente 1 und 5 von C sind verschieden.
6. Generieren Sie mithilfe des Burg-Koeffizientenvektors C die Vorhersagefehler.
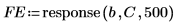
◦ Bei der Burg-Methode wird dem ersten P Fehler das Gewicht 0 zugewiesen, sodass die Minimierung hier im Gegensatz zur Minimierung nach der Yule-Walker-Methode nicht durch das Auffüllen der Stichprobe mit Nullen beeinflusst wird.
◦ Das Burg-Kriterium berücksichtigt zudem sowohl die Vorwärtsfehler FE als auch die Rückwärtsfehler BE.
7. Verwenden Sie die Funktionen response und reverse, um die Rückwärtsfehler zu berechnen.
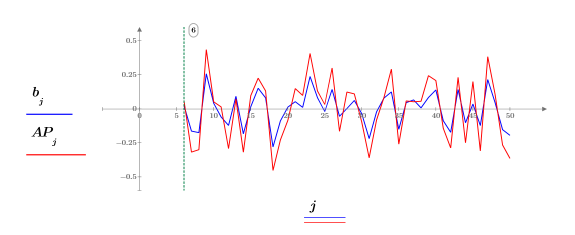
8. Verwenden Sie die Vorhersagefehler FE und die Autoregressionsfunktion b, um die eigentlichen Vorhersagen AP zu berechnen. Stellen Sie dann einen Teil der vorhergesagten und der tatsächlichen Reihe ab dem Ausdruck Pth grafisch dar.
Spektralschätzung
Sie können die von den linearen Vorhersagemethoden generierten Koeffizienten verwenden, um die spektrale Leistungsdichte der modellierten Prozesse zu schätzen. In diesem Kontext wird der Burg-Algorithmus auch als Maximum-Entropie-Methode der Spektralanalyse (MESA) bezeichnet. In einigen Fällen lassen sich damit die Spektren kurzer Zeitreihen genauer bestimmen als mit FFT.
Schätzen Sie die spektrale Leistungsdichte eines Prozesses, der aus einer Summe von sinusförmigen Signalen besteht, denen gaußsches Rauschen hinzugefügt wurde.
1. Definieren Sie mit der Funktion sin ein Signal, das zwei Sinus-Komponenten hat.
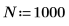
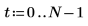
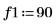
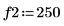
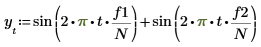
2. Verwenden Sie die Funktion gaussn, um Gaußsches Rauschen hinzuzufügen.
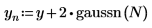
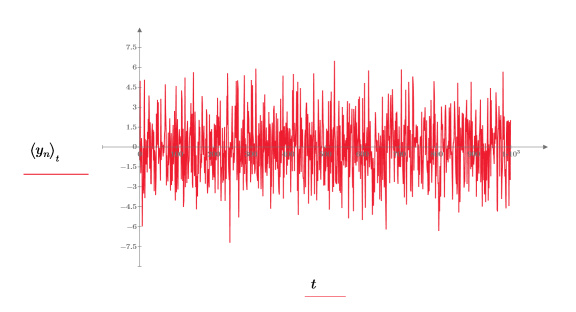
Die Funktion gaussn gibt einen n-Elementvektor von Zufallszahlen zurück, der eine gaußsche Wahrscheinlichkeitsverteilung mit dem Mittelwert 0 und der Standardabweichung 1 aufweist.
3. Legen Sie zwei Reihenfolgen für die lineare Extrapolation fest.
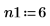
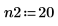
4. Verwenden Sie die Funktion burg, um das Spektrum mit autoregressiven Modellen der beiden Reihenfolgen zu schätzen, wobei die gesamte Zeitreihe als Stichprobe verwendet wird.
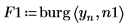
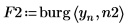
5. Berechnen Sie mit der Funktion gain die entsprechende spektrale Leistungsdichte als quadrierter Betrag der Übertragungsfunktion, die durch die Koeffizienten-Arrays F1 und F2 definiert wird.
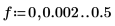
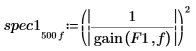
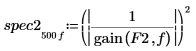
6. Stellen Sie die beiden spektralen Leistungsdichten grafisch dar.
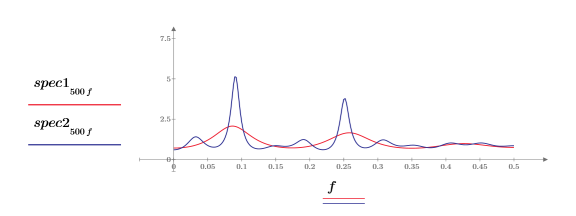
◦ Jede Potenzspektrum hat zwei Spitzenwerte.
◦ Die unteren und die oberen Frequenzspitzenwerte treten bei beiden Spektren bei ungefähr derselben Frequenz auf.
7. Unterteilen Sie die Kurven spec1 und spec2 jeweils in zwei Segmente, um die Suche nach den Spitzenwerten und den Frequenzen, bei denen diese auftreten, zu erleichtern.
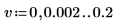 | 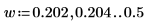 |
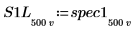 | 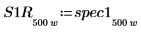 |
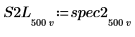 | 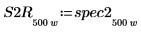 |
8. Definieren Sie mit der Funktion if eine Funktion, die die Frequenz zurückgibt, bei der das gegebene Segment einen Spitzenwert hat, und verwenden Sie sie, um die Spitzenwerte auf der linken und der rechten Seite jeder Spektrumsspurkurve zu suchen.
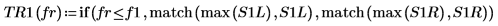 | |
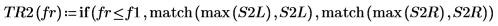 | |
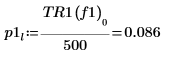 | 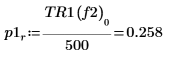 |
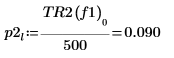 | 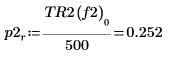 |
9. Verwenden Sie die Funktion max, um den Betrag der einzelnen Spitzenwerte zu berechnen.
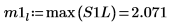 | 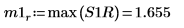 |
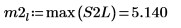 | 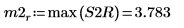 |
10. Plotten Sie jede Funktion unabhängig. Verwenden Sie horizontale und vertikale Markierungen, um den Betrag der einzelnen Spitzenwerte und die Frequenz anzuzeigen, bei der diese auftreten.
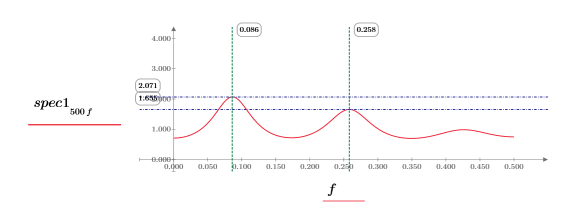
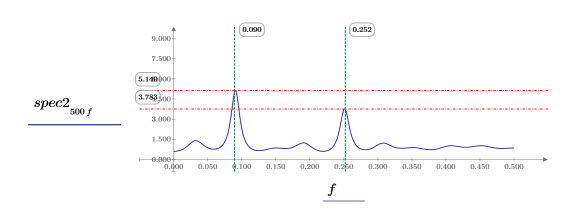
◦ Beobachten Sie die beiden Diagramme, während Sie das Arbeitsblatt neu berechnen.
◦ Der Betrag der Spitzenwerte ändert sich mit jeder Neuberechnung, und für gewöhnlich sind die Werte unterschiedlich. Es ist allerdings auch möglich, dass die Beträge gleich sind.
◦ Die Spitzenwerte treten etwa bei derselben Frequenz auf.
Nähere Informationen zu dieser Methode der Spektralschätzung finden Sie in Digital Spectral Analysis with Applications von S. Lawrence Marple, Jr. (Prentice-Hall, Inc).