Beispiel: Lineares Detrending

Funktionen > Signalverarbeitung > Zeitreihenanalyse > Beispiel: Lineares Detrending

Verwenden Sie die Funktion detrend, um einen linearen Trend mithilfe einer Kleinste-Quadrate-Mittelwertgeraden zu approximieren und aus Daten zu entfernen.

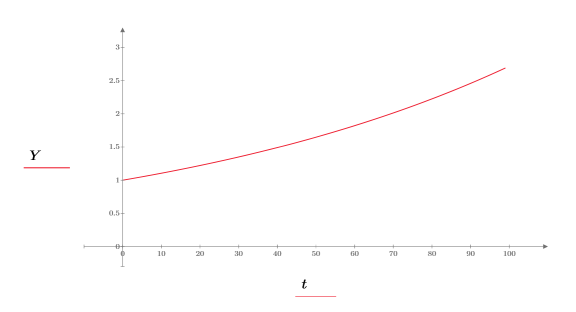
1. Definieren Sie ein Exponentialsignal.

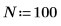
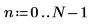
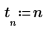
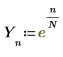
2. Plotten Sie das exponentielle Signal.

<region id="ID0E6EK4" actualWidth="575.69230769230762" actualHeight="312" top="307.20000000000005" left="38.400000000000006" height="312" width="575.69230769230762" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="90">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="479.692307692308" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="100">
          <axisLine position="origin" positionticmark="0" legendWidth="58.32" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="91">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
              </math>
              <math resultRef="92">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="3">
          <axisLine position="origin" positionticmark="0" legendWidth="63.57" />
          <axisGrid>
            <gridFrequency>7</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="99">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">Y</id>
              </math>
              <math resultRef="100">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="94">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="96">
              <real xmlns="http://schemas.mathsoft.com/math50">0.5</real>
            </secondTickValue>
            <endValue resultRef="98">
              <real xmlns="http://schemas.mathsoft.com/math50">3</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

3. Verwenden Sie die Funktion whiten, um dem Signal weißes Rauschen hinzuzufügen.

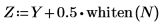
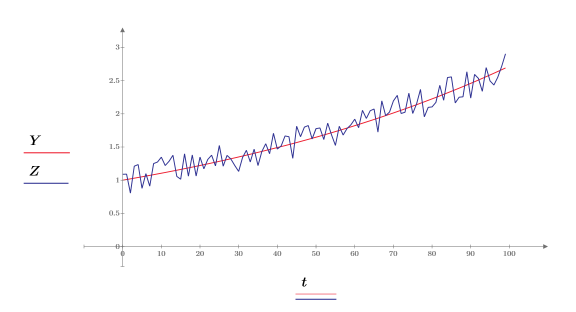
4. Plotten Sie das ursprüngliche Signal und das Signal mit dem Rauschen.

<region id="ID0ERIK4" actualWidth="576.00000000000011" actualHeight="312" top="864.00000000000011" left="38.400000000000006" height="312" width="576.00000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="110">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="111">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="480" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="100">
          <axisLine position="origin" positionticmark="0" legendWidth="58.32" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="112">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
              </math>
              <math resultRef="113">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="3">
          <axisLine position="origin" positionticmark="0" legendWidth="63.57" />
          <axisGrid>
            <gridFrequency>7</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="118">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">Y</id>
              </math>
              <math resultRef="119">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="120">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">Z</id>
              </math>
              <math resultRef="121">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="115">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="117">
              <real xmlns="http://schemas.mathsoft.com/math50">0.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

5. Wenden Sie die Funktion detrend auf das Signal mit dem Rauschen an.

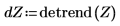
6. Plotten Sie die ursprüngliche Funktion und die trendbereinigte Funktion.

<region id="ID0EVLK4" actualWidth="575.69230769230762" actualHeight="312" top="1324.8000000000002" left="38.400000000000006" height="312" width="575.69230769230762" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="132">
          <traceStyle color="#FF00008B" symbol="none" line-weight="1" line-style="Solid">Linien</traceStyle>
        </trace>
        <trace resultRef="133">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="460.492307692308" height="254.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="100">
          <axisLine position="origin" positionticmark="1" legendWidth="58.32" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="134">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">t</id>
              </math>
              <math resultRef="135">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="3">
          <axisLine position="origin" positionticmark="0" legendWidth="70.9466666666667" />
          <axisGrid>
            <gridFrequency>8</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="140">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">Z</id>
              </math>
              <math resultRef="141">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="142">
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">dZ</id>
              </math>
              <math resultRef="143">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="137">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="139">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

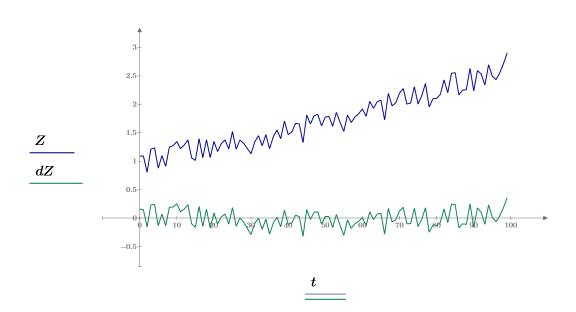
Der Wegfall des linearen Trends lässt sich weiter veranschaulichen, indem man die Kleinste-Quadrate-Gerade vor und nach der Entfernung des Trends betrachtet.

7. Verwenden Sie die Funktionen slope und intercept, um die Steigung und den Schnittpunkt vor und nach der Trendeliminierung zu berechnen.

<region id="ID0EGPK4" actualWidth="174.60000000000002" actualHeight="25.6" top="1804.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="152">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">Sz</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Steigung</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Z</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EUPK4" actualWidth="199.37333333333333" actualHeight="25.6" top="1843.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="154">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">Iz</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">intercept</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Z</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EGQK4" actualWidth="163.36" actualHeight="25.6" top="1881.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="156">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">Sdz</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Steigung</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">dZ</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EUQK4" actualWidth="188.13333333333335" actualHeight="25.6" top="1920.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="158">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">Idz</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">intercept</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">dZ</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

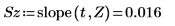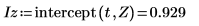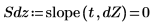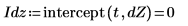Das ist immer der Fall. Die Ausgabe von detrend ist ein Vektor, dessen Kleinste-Quadrate-Gerade eine durch den Ursprung verlaufende horizontalen Linie ist, d.h. Steigung und Achsenabschnitt sind beide sehr nahe an 0.

Ein Effekt von detrend besteht darin, dass der Mittelwert aus den Eingabedaten entfernt wurde. Dies wird deutlich, wenn man den DC-Term vor und nach der Trendeliminierung betrachtet.

8. Verwenden Sie die Funktion dft, um den (ersten) DC-Term vor und nach der Trendeliminierung zu berechnen.

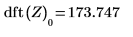
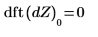
Die Funktion detrend führt eine einfache Vorverarbeitungsaufgabe aus, die dem Glätten häufig vorausgeht. Wie oben erwähnt, ist die Trendbereinigung häufig ein hilfreicher erster Schritt bei der Spektralschätzung.

Zugehörige Themen

Lineares Detrending

War dies hilfreich?