Beispiel: Interaktionen
Verwenden Sie die Funktion effects, um die Rolle von Interaktionen in Experimenten zu verstehen.
1. Erzeugen Sie mit der Funktion fullfact eine Konstruktionsmatrix aus zwei Faktoren.
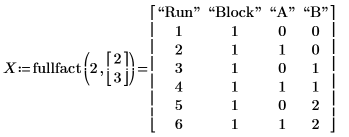
2. Geben Sie die reellen Werte für das Experiment in der Matrix Vals an. Der Faktor Gender (Geschlecht) ist in zwei Ebenen unterteilt: male (männlich) und female (weiblich). Der Faktor Age (Alter) ist in drei Ebenen unterteilt: young (jung), middle (mittel) und old (alt). Da die Faktoren nicht dieselbe Anzahl an Ebenen aufweisen, wird NaN in die erste Zeile von Vals eingefügt, um das leere Element aufzufüllen.
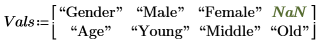
3. Sortieren Sie die Ergebnisse eines Experiments mit der Funktion doelabel nach Geschlecht und Alter.

Matrix X und D sind identisch, aber X zeigt die kodierten Werte der Faktoren, während D deren reelle Werte zeigt.
Ohne Interaktionen, nur ein signifikanter Faktor
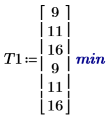
1. Zeichnen Sie die durchschnittliche Dauer auf, die jede Gruppe damit verbringt, eine Aufgabe zu lernen. Für Run 1 beträgt die mittlere Lernzeit junger Männer 9 Minuten.
2. Rufen Sie die Funktion effects auf, um die Wirkungen von Geschlecht, Alter und deren Wechselwirkung zu sehen.

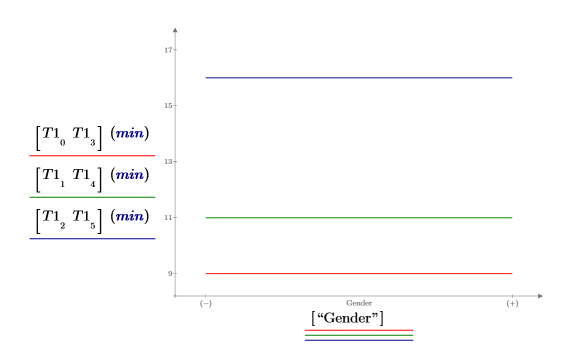
Die Teilmatrix Gender zeigt, dass das Geschlecht die Lernzeit nicht beeinflusst. Deshalb bestehen keine Interaktionswirkungen zwischen Alter und Geschlecht, für die ein Bericht erstellt werden könnte.
3. Erzeugen Sie ein Wirkungsdiagramm, um darzustellen, wie sich das Alter auf die Lernzeit auswirkt. Die jüngste Gruppe benötigt durchschnittlich 9 Minuten, um die Aufgabe zu erlernen.
Ohne Interaktionen, zwei signifikante Faktoren
1. Zeichnen Sie die durchschnittliche Dauer auf, die jede Gruppe damit verbringt, eine zweite Aufgabe zu lernen.
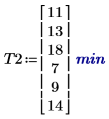
2. Rufen Sie die Funktion effects auf, um die Wirkungen von Geschlecht, Alter und deren Wechselwirkung zu sehen.

Der Einfluss des Alters auf den Lernprozess ist identisch mit dem bei der ersten Aufgabe. Dieses Mal haben jedoch männliche Personen länger gebraucht, die Aufgabe zu lernen, als weibliche Personen.
3. Um die Interaktionswirkungen von AB auf unterschiedlichen Ebenen von A und B zu berechnen, definieren Sie i und j als Ebenen von A und B sowie mABi, j als mittlere Reaktion für AB bei i und j.

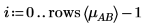
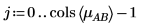
4. Berechnen Sie mit der Funktion mean den Gesamtmittelwert für dieses Experiment und den Mittelwert für jeden Faktor.
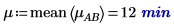
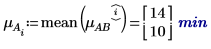
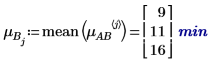
5. Berechnen Sie die Ebenenwirkungen für jeden Faktor.
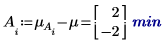
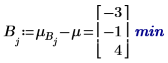
6. Berechnen Sie für jede Ebene der Faktoren A und B mithilfe der Funktion augment die additiven Faktorwirkungen, die der Summe des Gesamtmittelwerts des Experiments entsprechen, die Ebenenwirkung von A und die Ebenenwirkung von B für alle Ebenen von A und B.
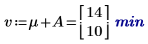
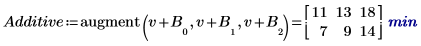
7. Berechnen Sie die Interaktionswirkungen oder den Unterschied zwischen der mittleren Antwort für AB und die additive Faktorwirkung für jede Ebene von A und B.
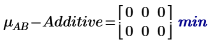
Für diese Aufgabe bestehen keine Interaktionswirkungen zwischen Alter und Geschlecht.
8. Plotten Sie die durchschnittliche Lernzeit für jedes Geschlecht. Junge weibliche Personen haben durchschnittlich 7 Minuten benötigt, um die zweite Aufgabe zu erlernen. Da keine Interaktionswirkungen zwischen Geschlecht und Alter bestehen, sind die beiden Kurven parallel.
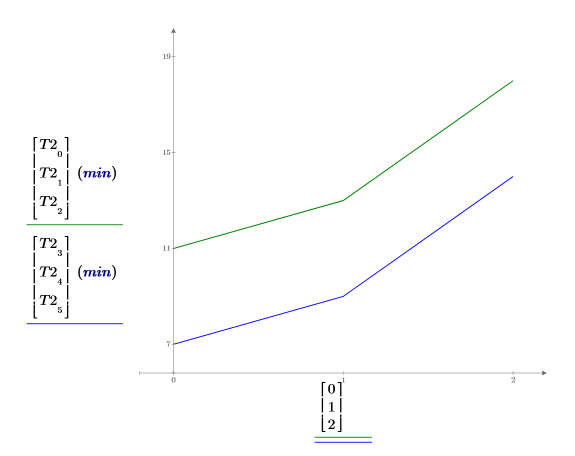
Mit wichtigen Interaktionen
1. Zeichnen Sie die durchschnittliche Dauer auf, die jede Gruppe damit verbringt, eine dritte Aufgabe zu lernen. Rufen Sie die Funktion effects auf, um die Wirkungen von Geschlecht, Alter und deren Wechselwirkung zu sehen.
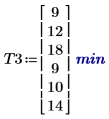

Der Einfluss des Alters ist identisch mit dem bei der ersten und zweiten Aufgabe, aber der Einfluss des Geschlechts ist geringer als für die zweite Aufgabe. Für diese dritte Aufgabe bestehen Interaktionswirkungen zwischen Alter und Geschlecht.
2. Berechnen Sie die Interaktionswirkungen.

3. Berechnen Sie mit der Funktion mean den Gesamtmittelwert für dieses Experiment und den Mittelwert für jeden Faktor.
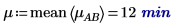
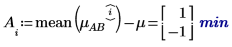
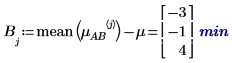
4. Berechnen Sie für jede Ebene der Faktoren A und B mithilfe der Funktion augment die additiven Faktorwirkungen, die der Summe des Gesamtmittelwerts des Experiments entsprechen, die Ebenenwirkung von A und die Ebenenwirkung von B für alle Ebenen von A und B.
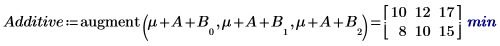
5. Berechnen Sie die Interaktionswirkungen oder den Unterschied zwischen der mittleren Antwort für AB und die additive Faktorwirkung für jede Ebene von A und B.
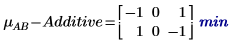
Es besteht ein Unterschied zwischen der mittleren Reaktion der Interaktion AB und der additiven Faktorwirkung.
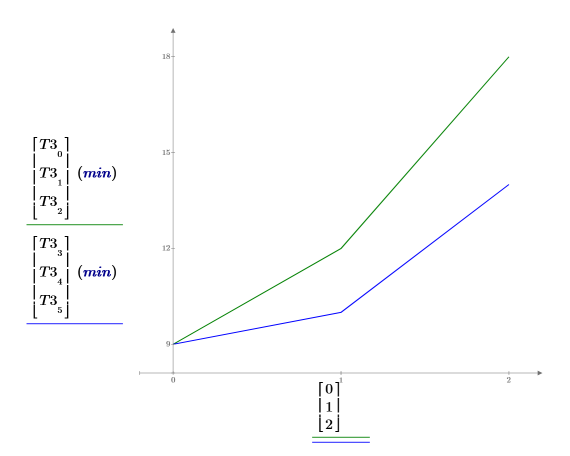
6. Plotten Sie die durchschnittliche Lernzeit für jedes Geschlecht. Während zwischen jungen männlichen und weiblichen Personen keine Unterschiede in der Leistung bestehen, benötigen alte männliche Personen mehr Zeit als alte weibliche Personen, die dritte Aufgabe zu lernen. Die beiden Kurven sind nicht parallel, da eine wichtige Interaktion zwischen dem Alter und dem Geschlecht besteht.
Mit unwichtigen Interaktionen
1. Zeichnen Sie die durchschnittliche Dauer auf, die jede Gruppe damit verbringt, eine vierte Aufgabe zu lernen.

2. Rufen Sie die Funktion effects auf, um die Wirkungen von Geschlecht, Alter und deren Wechselwirkung zu sehen.

Der Einfluss von Geschlecht und Alter ist sehr ähnlich zu dem bei der dritten Aufgabe.
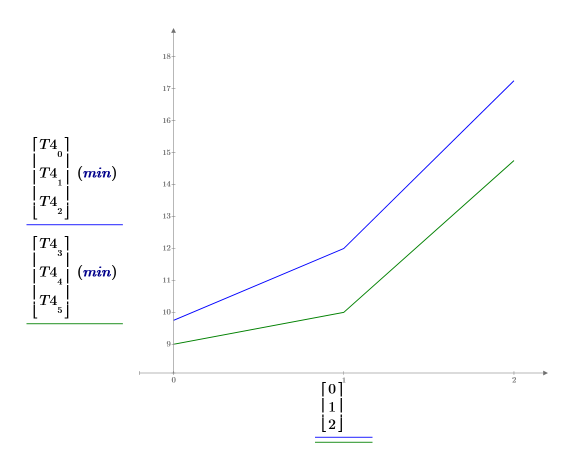
3. Plotten Sie die durchschnittliche Lernzeit für jedes Geschlecht. Die beiden Kurven sind fast parallel, was darauf hinweist, dass die Interaktion, die zwischen Alter und Geschlecht besteht, unwichtig ist.
Verweis
Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models, 4th ed., McGraw-Hill/Irwin, Boston, 1996, S. 803.