Beispiel: Grubbs-Methode zum Erkennen von Ausreißern
Teststatistik nach Grubbs
Berechnen Sie die Teststatistik nach Grubbs, wie sie von der Funktion Grubbs verwendet wird, um Ausreißer zu erkennen. Vergleichen Sie die Grubbs-Teststatistik mit der Teststatistik der Ausreißer.
1. Definieren Sie einen Datensatz, der ein Wärmeflussexperiment beschreibt, und stellen Sie ihn grafisch dar.
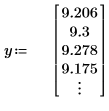
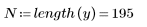
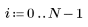
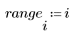
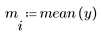
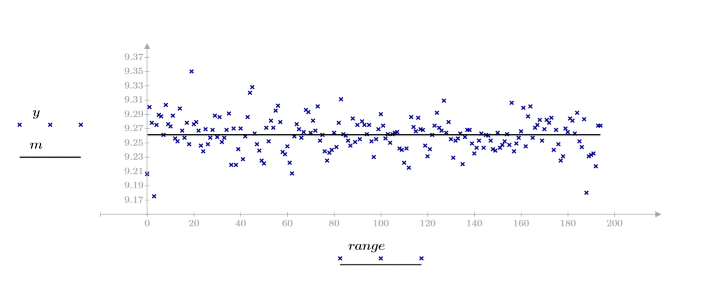
2. Definieren Sie den kritischen Wert der studentschen T-Verteilung mit N - 2 Freiheitsgraden und einem Signifikanzniveau von alpha/(2N).
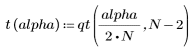
Die Funktion qt berechnet die inverse kumulative Wahrscheinlichkeitsverteilung der studentschen T-Verteilung. |
3. Definieren Sie die Grubbs-Teststatistik als Funktion von Alpha.
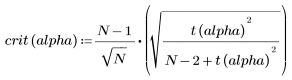
4. Definieren Sie das Signifikanzniveau für einen Vertrauensbereich von 90 %.
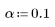
5. Rufen Sie die Funktion Grubbs auf, um Ausreißer zu ermitteln.
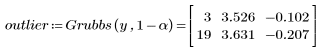
Die Funktion Grubbs kann eine Matrix als Eingabe akzeptieren. In diesem Fall gibt sie verschachtelte Paare von Indizes für die Array-Positionen der Ausreißer zurück.
6. Vergleichen Sie die Grubbs-Teststatistik mit den Teststatistiken der Ausreißer.

Die beiden Ausreißer verfügen über eine Teststatistik, die größer als die Grubbs-Teststatistik ist. Auch wenn mehrere Indizes zurückgegeben werden, bedeutet dies nicht, dass alle Kandidaten Ausreißer sein müssen. Dies liegt daran, dass sich der kritische Wert und die Teststatistik ändern, wenn ein Kandidat entfernt wird. Beide sind von N abhängig.
Da beim Grubbs-Test davon ausgegangen wird, dass die Daten normal sind, lohnt es sich zu prüfen, ob ihre Daten einer Normalverteilung folgen. Sie können beispielsweise einen visuellen Test wie den normalen Wahrscheinlichkeitsplot verwenden, bevor Sie fortfahren.
GrubbsClassic
Verwenden Sie die Funktion GrubbsClassic, um den Punkt zu ermitteln, der in einem Datensatz der wahrscheinlichste Ausreißer ist.
1. Berechnen Sie die Teststatistik, die für den Datensatz oben die größte ist.
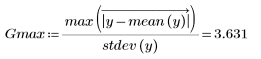
2. Definieren Sie Alpha für ein Konfidenzintervall von 98 %.
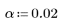
3. Vergleichen Sie die Grubbs-Teststatistik mit Gmax.
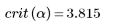
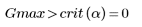
Auf diesem Signifikanzniveau werden keine Ausreißer erkannt.
4. Rufen Sie die Funktion GrubbsClassic auf.
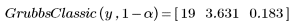
Der von GrubbsClassic zurückgegebene Punkt ist kein Ausreißer, aber es handelt sich dabei um den Datenpunkt, der der wahrscheinlichste Ausreißer ist.
Begrenzte Wahrscheinlichkeit für das Erkennen von Ausreißern
Verwenden Sie das besondere Konstrukt root, um die begrenzte Wahrscheinlichkeit zu berechnen, mit der Ausreißer erkannt werden.
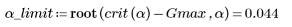
Ausreißer werden erkannt, wenn Alpha größer als α_limit oder das Konfidenzintervall mit anderen Worten ausgedrückt kleiner als (1 - α_limit) ist:
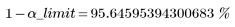
Dies stimmt mit den oben ermittelten Ergebnissen überein. Für ein Konfidenzintervall von 98 % wurden keine Ausreißer erkannt, aber zwei Ausreißer für ein Konfidenzintervall von 90 %.