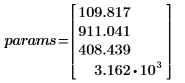Beispiel: Gradienten-Operator
• Definieren Sie eine Funktion f:
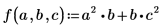
Verwenden Sie den Gradienten-Operator, um einen Vektor partieller Ableitungen für f zu erhalten:
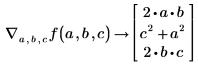
• Definieren Sie eine Vektorfunktion, und berechnen Sie den Gradienten der Funktion f mit dem Vektor x.
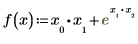

In diesem Beispiel ist ORIGIN, das den Startindex für alle Arrays festlegt, auf 0 festgelegt.
Die Variable mit dem größten tiefgestellten Index in f ist x2. Mathcad geht davon aus, dass es drei Variablen gibt: x0, x1 und x2. Dies ergibt einen Gradientenvektor mit drei Werten, welche die partiellen Ableitungen dieser Variablen enthält. Wenn entweder x0 oder x1 nicht in f vorkommt, gibt Mathcad trotzdem einen Vektor mit drei Werten zurück, aber die Einträge, die den fehlenden Variablen entsprechen, werden auf 0 gesetzt.
Für den größten tiefgestellten Index in f, n, nimmt Mathcad n + 1 Variablen x0, x1, ... xn an, und gibt einen Vektor der Länge n + 1 zurück.
• Wenn Sie x numerisch definieren, können Sie den Gradienten mit dem Gleichheitszeichen = auswerten. Mathcad wertet den Gradienten an den Werten in x aus und gibt einen Vektor aus Zahlen zurück, der den Gradienten am Punkt x darstellt. Die Länge von x muss größer sein als der größte tiefgestellte Index in f, und Mathcad gibt einen Gradienten mit Länge(x)-Einträgen zurück.
Im folgenden Beispiel sind x0 und x1 die einzigen Variablen, die in dem Ausdruck vorkommen. Mathcad nimmt die partiellen Ableitungen nach x0 und x1 und gibt einen Vektor mit zwei Werten zurück.
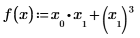
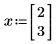
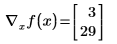
Wenn Sie jedoch x als einen Vektor mit drei Elementen definieren, geht Mathcad davon aus, dass es eine zusätzliche Variable, x2, gibt, die nicht im Ausdruck erscheint. Das Ergebnis ist ein Vektor aus drei Elementen.
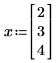
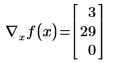
Gradienten-Operator mit der Funktion "genfit" verwenden
Der Gradienten-Operator eignet sich besonders zum Einrichten der Argumente für die Funktion genfit, die eine allgemeine nichtlineare Funktion in einen Datensatz einpasst.
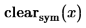
• Verwenden Sie die Daten in der folgenden Tabelle.
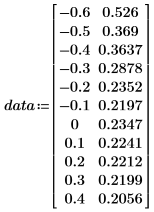
• Die erste Spalte enthält die x-Werte der Daten, die zweite Spalte die y-Werte.
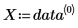
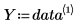
• Modellieren Sie die Daten mit einer Funktion der folgenden Form:
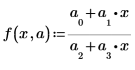
Hier sind a1, a2 und a3 unbekannte Parameter, die im Vektor a enthalten sind.
Sie können die Daten modellieren, indem Sie genfit wie folgt aufrufen:
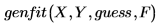
In diesem Ausdruck
◦ sind X und Y Vektoren, die die x-Werte und die y-Werte der Daten enthalten.
◦ guess ist ein Vektor von Anfangsschätzwerten für die Parameter.
◦ F ist ein Vektor, dessen erster Eintrag die Modellierungsfunktion f(x, a) ist und dessen übrige Einträge die partiellen Ableitungen von f in Bezug auf die unbekannten Parameter sind.
• Erstellen Sie den Vektor F mit dem Gradienten-Operator und der Funktion stack.
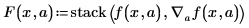

• Die Funktion stack setzt die Modellierungsfunktion f auf den durch den Gradienten-Operator erzeugten Vektor partieller Ableitungen.
• Erstellen Sie als Nächstes einen Schätzvektor für die Parameter.
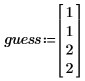
• Wenden Sie genfit wie folgt an:
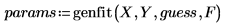
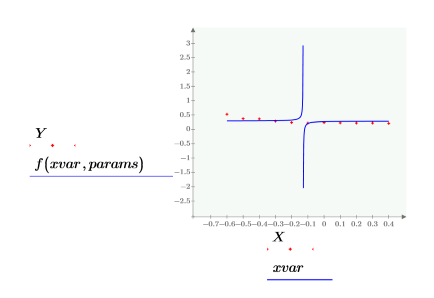
• Diese Parameter ergeben die Bestapproximation: