Beispiel: Funktionen der geometrischen und hypergeometrischen Verteilung
Geometrische Verteilung
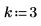
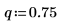
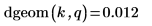
2. Verwenden Sie die Funktion pgeom, um die kumulative Wahrscheinlichkeitsverteilung für den Wert k zu berechnen:
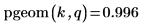
3. Verwenden Sie die Funktion pgeom, um die umgekehrte kumulative Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeit p zu berechnen:
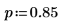
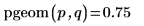
4. Verwenden Sie die Funktion rgeom, um einen Vektor von m Zufallszahlen zu erzeugen, die die geometrische Verteilung aufweisen:
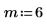

Die Neuberechnung des Arbeitsblatts bewirkt, dass die Funktion rgeom einen neuen Satz von Zufallszahlen zurückgibt.
Hypergeometrische Verteilung
1. Definieren Sie die Eingabeparameter a, b, m und n. Bei den Parametern handelt es sich um Ganzzahlen, für die folgende Beziehung gilt:
max{0, n − b} ≤ m ≤ min{n, a}, und 0 für m an anderer Stelle.
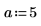
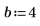
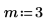
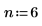
2. Verwenden Sie die Funktion dhypergeom, um die Wahrscheinlichkeitsdichte für die hypergeometrische Verteilung zu berechnen:
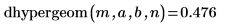
3. Verwenden Sie die Funktion phypergeom, um die kumulative Wahrscheinlichkeitsverteilung zu berechnen:
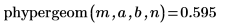
4. Verwenden Sie die Funktion qhypergeom, um die umgekehrte kumulative Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeit p zu berechnen:
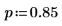
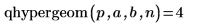
5. Verwenden Sie die Funktion rhypergeom, um einen Vektor von m Zufallszahlen zu erzeugen, die die hypergeometrische Verteilung aufweisen:
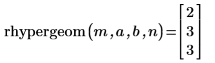
Die Neuberechnung des Arbeitsblatts bewirkt, dass die Funktion rhypergeom einen neuen Satz von Zufallszahlen zurückgibt.