Hypergeometrische Verteilung
Der hypergeometrischen Gleichung sind die folgenden Funktionen zugeordnet:
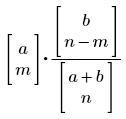
Die Parameter m, n, a und b sind Ganzzahlen, die max{0, n − b} ≤ m ≤ min{n, a} entsprechen und 0 für m überall sonst.
• dhypergeom(m, a, b, n) – Gibt die Wahrscheinlichkeitsdichte für die hypergeometrische Verteilung zurück.
• phypergeom(m, a, b, n) – Gibt die kumulative Wahrscheinlichkeitsverteilung zurück.
• qhypergeom(p, a, b, n) – Gibt die inverse kumulative Wahrscheinlichkeitsverteilung für den Wert p zurück.
• rhypergeom(m, a, b, n) – Gibt einen Vektor von m Zufallszahlen mit hypergeometrischer Verteilung zurück.
Argumente
• m, n, a, b sind Ganzzahlen, wobei gilt: 0 ≤ m ≤ a, 0 ≤ n − m ≤ b , 0 ≤ n ≤ a + b. Um eine Integration und andere Operationen mit diesen Argumenten zu ermöglichen, sind Werte außerhalb des angegebenen Bereichs zulässig, geben jedoch als Ergebnis 0 zurück.
• p ist eine reelle Wahrscheinlichkeit, 0 ≤ p ≤ 1.