Beispiel: Generieren von Zufallszahlen

Funktionen > Statistik > Wahrscheinlichkeitsverteilungen > Beispiel: Generieren von Zufallszahlen

Erzeugen Sie Vektoren mit gleich-, normal- und exponentialverteilten Zufallszahlen über einem Intervall.

Gleichförmig verteilt

1. Rufen Sie die Funktion runif auf, um n_set Zufallszahlen zu generieren, die zwischen niedrigen und hohe Werten gleichförmig verteilt sind.

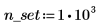
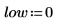
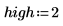
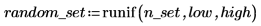
2. Verwenden Sie die Funktion hist, um ein Histogramm des gleichförmigen Satzes mit n_bins Bins zu generieren, und berechnen Sie anschließend den Mittelwert des Satzes.

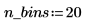
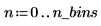
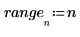
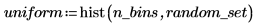
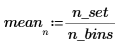
3. Plotten Sie das Histogramm, und zeigen Sie den erwarteten Mittelwert des Datensatzes an:

<region id="ID0ELA3BB" top="480.00000000000006" left="38.400000000000006" height="216" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="202">
          <traceStyle color="#FF31ADC2" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
        <trace resultRef="203">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="437.6" height="158.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="0" legendWidth="92.1466666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="208">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="209">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="205">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="207">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="75">
          <axisLine position="origin" positionticmark="0" legendWidth="111.033333333333" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="216">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">uniform</id>
              </math>
              <math resultRef="217">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="218">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">mean</id>
              </math>
              <math resultRef="219">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="211">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="213">
              <real xmlns="http://schemas.mathsoft.com/math50">15</real>
            </secondTickValue>
            <endValue resultRef="215">
              <real xmlns="http://schemas.mathsoft.com/math50">67</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

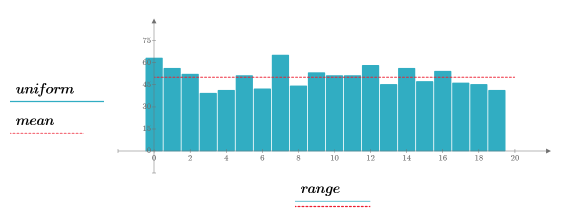
Um einen neuen Zufallszahlensatz abzurufen, klicken Sie auf der Registerkarte Berechnung in der Gruppe Steuerelemente auf Berechnen. Ein neuer Startwert wird verwendet, um bei jeder Neuberechnung Zufallszahlen zu generieren.

Normalverteilt

1. Rufen Sie die Funktion rnorm auf, um n_set Zufallszahlen zu generieren, die die Normalverteilung mit dem Mittelwert μ und der Standardabweichung σ aufweisen.

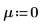
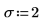
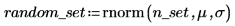
2. Verwenden Sie die Funktionen floor, ceil, min und max, um den minimalen und den maximalen Bereich des Datensatzes zu berechnen, und berechnen Sie anschließend die Breite jedes Bins:

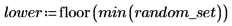
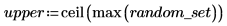
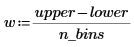
3. Legen Sie den horizontalen Maßstab für das Diagramm fest:

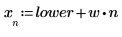
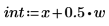
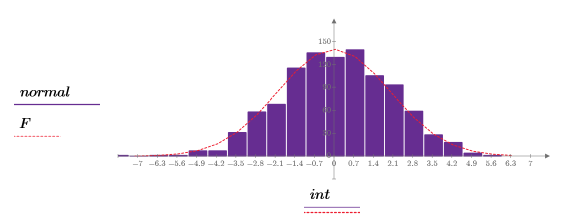
4. Rufen Sie die Funktion dnorm auf, um die für den Datensatz erwartete Normalverteilung F zu berechnen. Plotten Sie anschließend ein Histogramm des normalen Satzes mit n_bins Bins.

<region id="ID0EON3BB" top="1344.0000000000002" left="38.400000000000006" height="36.800000000000004" width="227.07666666666668" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="247">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <indexer />
        <id labels="*" xml:space="preserve">F</id>
        <id labels="*" xml:space="preserve">n</id>
      </apply>
      <apply>
        <mult />
        <apply>
          <mult />
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n_set</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">w</id>
        </apply>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">dnorm</id>
          <sequence>
            <apply>
              <indexer />
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">int</id>
              <id xml:space="preserve">n</id>
            </apply>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">μ</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">σ</id>
          </sequence>
        </apply>
      </apply>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EKO3BB" top="1401.6000000000001" left="38.400000000000006" height="222.00000000000003" width="575" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="251">
          <traceStyle color="#FF662D91" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
        <trace resultRef="252">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="436.6" height="164.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-7" end="7">
          <axisLine position="origin" positionticmark="0" legendWidth="72.65" />
          <axisGrid>
            <gridFrequency>21</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="259">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">int</id>
              </math>
              <math resultRef="260">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="254">
              <real xmlns="http://schemas.mathsoft.com/math50">-7.0</real>
            </startValue>
            <secondTickValue resultRef="256">
              <real xmlns="http://schemas.mathsoft.com/math50">-6.3</real>
            </secondTickValue>
            <endValue resultRef="258">
              <real xmlns="http://schemas.mathsoft.com/math50">7.0</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="150">
          <axisLine position="origin" positionticmark="10" legendWidth="102.85" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="267">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">normal</id>
              </math>
              <math resultRef="268">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="269">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">F</id>
              </math>
              <math resultRef="270">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="262">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="264">
              <real xmlns="http://schemas.mathsoft.com/math50">30</real>
            </secondTickValue>
            <endValue resultRef="266">
              <real xmlns="http://schemas.mathsoft.com/math50">150</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

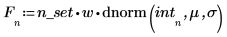
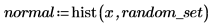
Exponentiell verteilt

1. Rufen Sie die Funktion rexp auf, um einen Satz an Zufallszahlen zu generieren, die mit der Rate r exponentiell verteilt sind.

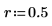
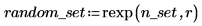
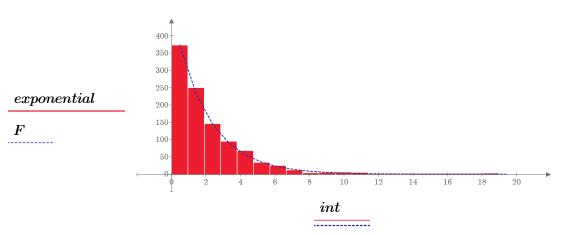
2. Rufen Sie die Funktion dexp auf, um die für den Datensatz erwartete Exponentialverteilung F zu berechnen. Plotten Sie anschließend ein Histogramm des Exponentialsatzes mit n_bins Bins.

<region id="ID0ELW3BB" top="2131.2000000000003" left="38.400000000000006" height="235" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="301">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">columns</traceStyle>
        </trace>
        <trace resultRef="302">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="418.4" height="177.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="0" legendWidth="72.65" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="307">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">int</id>
              </math>
              <math resultRef="308">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="304">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="306">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="400">
          <axisLine position="origin" positionticmark="0" legendWidth="133.973333333333" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="315">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">exponential</id>
              </math>
              <math resultRef="316">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="317">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">F</id>
              </math>
              <math resultRef="318">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="310">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="312">
              <real xmlns="http://schemas.mathsoft.com/math50">50</real>
            </secondTickValue>
            <endValue resultRef="314">
              <real xmlns="http://schemas.mathsoft.com/math50">400</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

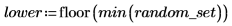
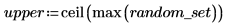
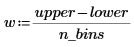
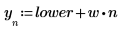
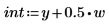
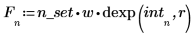
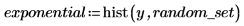
3. Rufen Sie die Funktionen pexp und qexp auf, um die kumulative Wahrscheinlichkeitsverteilung für den Wert x bzw. die umgekehrte kumulative Wahrscheinlichkeitsverteilung für den Wert p zu berechnen und zu plotten.

<region id="ID0E2Z3BB" top="2611.2000000000003" left="38.400000000000006" height="254.20000000000002" width="576" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="334">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="335">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Dash">Linien</traceStyle>
        </trace>
        <trace resultRef="336">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="476" height="177.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="0" legendWidth="72.65" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="341">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">int</id>
              </math>
              <math resultRef="342">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="338">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <endValue resultRef="340">
              <real xmlns="http://schemas.mathsoft.com/math50">20</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="1000">
          <axisLine position="origin" positionticmark="0" legendWidth="71.24" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <general precision="3" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="349">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">F</id>
              </math>
              <math resultRef="350">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="351">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Fp</id>
              </math>
              <math resultRef="352">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="353">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">Fq</id>
              </math>
              <math resultRef="354">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="344">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="346">
              <real xmlns="http://schemas.mathsoft.com/math50">100</real>
            </secondTickValue>
            <endValue resultRef="348">
              <real xmlns="http://schemas.mathsoft.com/math50">1000</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

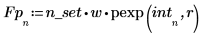
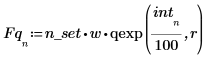
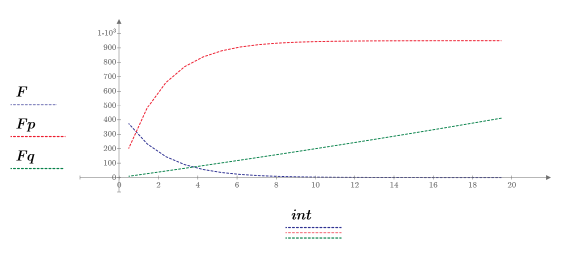
Das erste Argument der Funktion qexp ist die Wahrscheinlichkeit und muss kleiner als 1 sein, daher die Teilung von int durch 100.

Zugehörige Themen

Gleichmäßige Verteilung

Normalverteilung

Exponentialverteilung

War dies hilfreich?