Beispiel: Anpassen einer Modellierungsfunktion an Daten
Testen Sie, wie gut Ihre Daten von einer linearen, quadratischen oder exponentiellen Funktion modelliert werden.
1. Definieren Sie einen Datensatz.
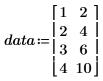
2. Erfassen Sie Spalte 0 und Spalte 1 in unabhängigen Vektoren.
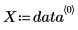
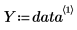
Lineare Anpassung
1. Verwenden Sie die Funktionen intercept und slope, um den Achsenabschnitt und die Steigungswerte zu ermitteln.
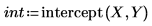
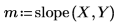
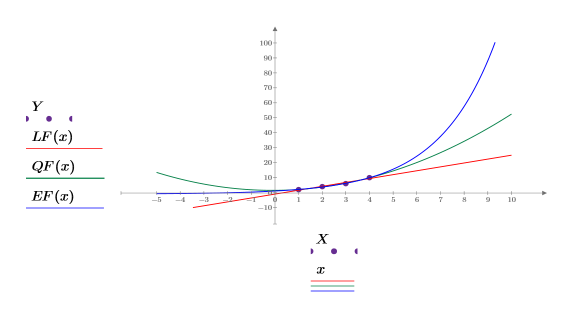
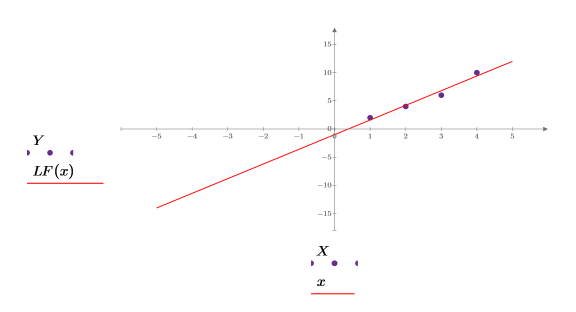
2. Stellen Sie die lineare Anpassungsfunktion LF zusammen mit X und Y grafisch dar.
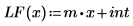
Quadratische Anpassung
1. Legen Sie den Polynomgrad fest.
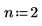
2. Verwenden Sie die Funktion polyfit, um die Anpassungsfunktion zu berechnen.
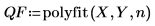
◦ In vorherigen Versionen dieses Beispiels wurde die abgelehnte Funktion regress verwendet, um eine Matrix von Koeffizienten zu erhalten. Diese Matrix wird anschließend der Funktion interp übergeben, um die Anpassungsfunktion zu erhalten.
◦ Die Funktion polyfit, die als Alternative zur veralteten Funktion regress empfohlen wird, gibt die Anpassungsfunktion zurück. Damit ist es nicht mehr notwendig, die Funktion interp zu verwenden.
◦ Ändern Sie versuchsweise den Wert des Polynomgrades, um festzustellen, wie sich dies auf die Anpassungsfunktion auswirkt (siehe Diagramm unten).
3. Plotten Sie die quadratische Anpassungsfunktion QF.
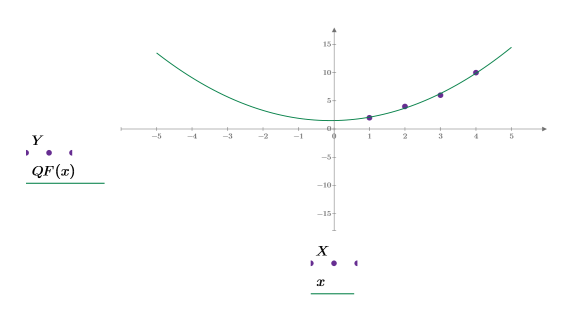
Exponentielle Anpassung
Die exponentielle Anpassungsfunktion wird durch Folgendes dargestellt:
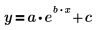
1. Stellen Sie Schätzwerte für die Parameter a, b und c bereit.
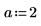 | 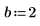 | 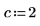 |
2. Definieren Sie den Schätzvektor.
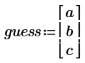
3. Verwenden Sie die Funktion expfit, um die drei Koeffizienten der Exponentialkurve zu berechnen.
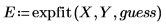
4. Plotten Sie die exponentielle Anpassungsfunktion EF.
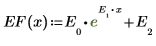
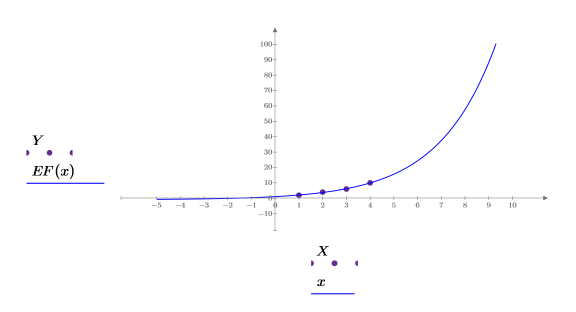
5. Zeigen Sie die drei grafischen Darstellungen an, um zu ermitteln, wie gut jedes Anpassungsmodell die Daten anpasst.