Beispiel: Elliptische Integralfunktion

Funktionen > Symbolische Funktionen > Beispiel: Elliptische Integralfunktion

Ableitungen elliptischer Integralfunktionen berechnen

• Vollständiges elliptisches Integral erster Art:

<region id="ID0EASYCB" actualWidth="410.26166666666671" actualHeight="53.743333445231123" top="57.600000000000009" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="16">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">m</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticK</id>
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <plus />
            <apply>
              <neg />
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
                <id xml:space="preserve" labels="VARIABLE">m</id>
              </apply>
            </apply>
            <apply>
              <mult />
              <parens>
                <apply>
                  <minus />
                  <real>1</real>
                  <id xml:space="preserve" labels="VARIABLE">m</id>
                </apply>
              </parens>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticK</id>
                <id xml:space="preserve" labels="VARIABLE">m</id>
              </apply>
            </apply>
          </apply>
          <apply>
            <minus />
            <apply>
              <mult />
              <real>2</real>
              <apply>
                <pow />
                <id xml:space="preserve" labels="VARIABLE">m</id>
                <real>2</real>
              </apply>
            </apply>
            <apply>
              <mult />
              <real>2</real>
              <id xml:space="preserve" labels="VARIABLE">m</id>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

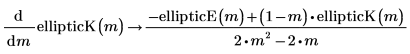
• Zweite Ableitung des vollständigen elliptischen Integrals erster Art:

<region id="ID0EQTYCB" actualWidth="547.04666666666674" actualHeight="53.743333445231123" top="115.20000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="17">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">m</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticK</id>
            <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
          </apply>
        </lambda>
        <degree>
          <real>2</real>
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <plus />
            <apply>
              <mult />
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <real>4</real>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </apply>
                  <real>2</real>
                </apply>
              </parens>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
                <id xml:space="preserve" labels="VARIABLE">m</id>
              </apply>
            </apply>
            <apply>
              <mult />
              <parens>
                <apply>
                  <plus />
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <real>3</real>
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                        <real>2</real>
                      </apply>
                    </apply>
                    <apply>
                      <mult />
                      <real>5</real>
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                    </apply>
                  </apply>
                  <real>2</real>
                </apply>
              </parens>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticK</id>
                <id xml:space="preserve" labels="VARIABLE">m</id>
              </apply>
            </apply>
          </apply>
          <apply>
            <plus />
            <apply>
              <minus />
              <apply>
                <mult />
                <real>4</real>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE">m</id>
                  <real>4</real>
                </apply>
              </apply>
              <apply>
                <mult />
                <real>8</real>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE">m</id>
                  <real>3</real>
                </apply>
              </apply>
            </apply>
            <apply>
              <mult />
              <real>4</real>
              <apply>
                <pow />
                <id xml:space="preserve" labels="VARIABLE">m</id>
                <real>2</real>
              </apply>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

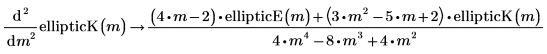
• Erste Ableitung durch m des unvollständigen elliptischen Integrals erster Art:

<region id="ID0EEVYCB" actualWidth="644.71433364629752" actualHeight="62.057867054653173" top="172.8" left="38.400000000000006" width="644.71433364629752" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="18">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">m</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
            <sequence>
              <id xml:space="preserve">z</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
            </sequence>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <plus />
          <apply>
            <neg />
            <apply>
              <div />
              <apply>
                <plus />
                <apply>
                  <mult />
                  <parens>
                    <apply>
                      <minus />
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                      <real>1</real>
                    </apply>
                  </parens>
                  <apply>
                    <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
                    <sequence>
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                    </sequence>
                  </apply>
                </apply>
                <apply>
                  <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
                  <sequence>
                    <id xml:space="preserve" labels="VARIABLE">z</id>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </sequence>
                </apply>
              </apply>
              <apply>
                <minus />
                <apply>
                  <mult />
                  <real>2</real>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                    <real>2</real>
                  </apply>
                </apply>
                <apply>
                  <mult />
                  <real>2</real>
                  <id xml:space="preserve" labels="VARIABLE">m</id>
                </apply>
              </apply>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <mult />
              <id xml:space="preserve" labels="VARIABLE">z</id>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <real>2</real>
                    </apply>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
            <apply>
              <mult />
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </apply>
                  <real>2</real>
                </apply>
              </parens>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <parens>
                      <apply>
                        <mult />
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                        <apply>
                          <pow />
                          <id xml:space="preserve" labels="VARIABLE">z</id>
                          <real>2</real>
                        </apply>
                      </apply>
                    </parens>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

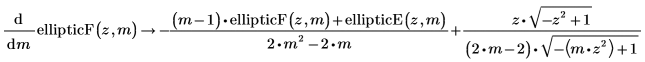
• Erste Ableitung durch z des unvollständigen elliptischen Integrals erster Art:

<region id="ID0EYWYCB" actualWidth="332.46700062592834" actualHeight="58.587600193993254" top="230.40000000000003" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="19">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">z</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
            <sequence>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">z</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
            </sequence>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <div />
          <real>1</real>
          <apply>
            <mult />
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <plus />
                <apply>
                  <neg />
                  <parens>
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="VARIABLE">z</id>
                        <real>2</real>
                      </apply>
                    </apply>
                  </parens>
                </apply>
                <real>1</real>
              </apply>
            </apply>
            <apply>
              <nthRoot />
              <placeholder />
              <apply>
                <plus />
                <apply>
                  <neg />
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="VARIABLE">z</id>
                    <real>2</real>
                  </apply>
                </apply>
                <real>1</real>
              </apply>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

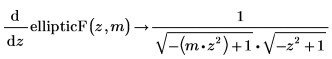
• Zweite Ableitung durch m des unvollständigen elliptischen Integrals erster Art:

<region id="ID0EMYYCB" actualWidth="1076.9693336462976" actualHeight="62.057867054653173" top="307.20000000000005" left="57.600000000000009" width="1076.9693336462976" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="20">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">m</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
            <sequence>
              <id xml:space="preserve">z</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
            </sequence>
          </apply>
        </lambda>
        <degree>
          <real>2</real>
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <minus />
          <apply>
            <div />
            <apply>
              <plus />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <plus />
                    <apply>
                      <minus />
                      <apply>
                        <mult />
                        <real>3</real>
                        <apply>
                          <pow />
                          <id xml:space="preserve" labels="VARIABLE">m</id>
                          <real>2</real>
                        </apply>
                      </apply>
                      <apply>
                        <mult />
                        <real>5</real>
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                      </apply>
                    </apply>
                    <real>2</real>
                  </apply>
                </parens>
                <apply>
                  <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
                  <sequence>
                    <id xml:space="preserve" labels="VARIABLE">z</id>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </sequence>
                </apply>
              </apply>
              <apply>
                <mult />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <real>4</real>
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                    </apply>
                    <real>2</real>
                  </apply>
                </parens>
                <apply>
                  <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
                  <sequence>
                    <id xml:space="preserve" labels="VARIABLE">z</id>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </sequence>
                </apply>
              </apply>
            </apply>
            <apply>
              <plus />
              <apply>
                <minus />
                <apply>
                  <mult />
                  <real>4</real>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                    <real>4</real>
                  </apply>
                </apply>
                <apply>
                  <mult />
                  <real>8</real>
                  <apply>
                    <pow />
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                    <real>3</real>
                  </apply>
                </apply>
              </apply>
              <apply>
                <mult />
                <real>4</real>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE">m</id>
                  <real>2</real>
                </apply>
              </apply>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <mult />
              <parens>
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <minus />
                        <apply>
                          <mult />
                          <real>4</real>
                          <apply>
                            <pow />
                            <id xml:space="preserve" labels="VARIABLE">m</id>
                            <real>2</real>
                          </apply>
                        </apply>
                        <apply>
                          <mult />
                          <real>2</real>
                          <id xml:space="preserve" labels="VARIABLE">m</id>
                        </apply>
                      </apply>
                    </parens>
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <real>3</real>
                    </apply>
                  </apply>
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <minus />
                        <real>1</real>
                        <apply>
                          <mult />
                          <real>3</real>
                          <id xml:space="preserve" labels="VARIABLE">m</id>
                        </apply>
                      </apply>
                    </parens>
                    <id xml:space="preserve" labels="VARIABLE">z</id>
                  </apply>
                </apply>
              </parens>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <real>2</real>
                    </apply>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
            <apply>
              <mult />
              <parens>
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <plus />
                        <apply>
                          <minus />
                          <apply>
                            <mult />
                            <real>4</real>
                            <apply>
                              <pow />
                              <id xml:space="preserve" labels="VARIABLE">m</id>
                              <real>4</real>
                            </apply>
                          </apply>
                          <apply>
                            <mult />
                            <real>8</real>
                            <apply>
                              <pow />
                              <id xml:space="preserve" labels="VARIABLE">m</id>
                              <real>3</real>
                            </apply>
                          </apply>
                        </apply>
                        <apply>
                          <mult />
                          <real>4</real>
                          <apply>
                            <pow />
                            <id xml:space="preserve" labels="VARIABLE">m</id>
                            <real>2</real>
                          </apply>
                        </apply>
                      </apply>
                    </parens>
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <real>2</real>
                    </apply>
                  </apply>
                  <parens>
                    <apply>
                      <minus />
                      <apply>
                        <minus />
                        <apply>
                          <mult />
                          <real>8</real>
                          <apply>
                            <pow />
                            <id xml:space="preserve" labels="VARIABLE">m</id>
                            <real>2</real>
                          </apply>
                        </apply>
                        <apply>
                          <mult />
                          <real>4</real>
                          <apply>
                            <pow />
                            <id xml:space="preserve" labels="VARIABLE">m</id>
                            <real>3</real>
                          </apply>
                        </apply>
                      </apply>
                      <apply>
                        <mult />
                        <real>4</real>
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                      </apply>
                    </apply>
                  </parens>
                </apply>
              </parens>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <parens>
                      <apply>
                        <mult />
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                        <apply>
                          <pow />
                          <id xml:space="preserve" labels="VARIABLE">z</id>
                          <real>2</real>
                        </apply>
                      </apply>
                    </parens>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

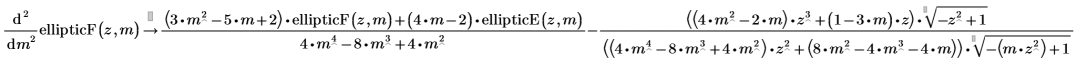
• Erste Ableitungen durch m und z des unvollständigen elliptischen Integrals zweiter Art:

<region id="ID0EE1YCB" actualWidth="395.08500000000004" actualHeight="53.743333445231123" top="364.80000000000007" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="21">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">m</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
            <sequence>
              <id xml:space="preserve">z</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
            </sequence>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <plus />
            <apply>
              <neg />
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
                <sequence>
                  <id xml:space="preserve" labels="VARIABLE">z</id>
                  <id xml:space="preserve" labels="VARIABLE">m</id>
                </sequence>
              </apply>
            </apply>
            <apply>
              <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
              <sequence>
                <id xml:space="preserve" labels="VARIABLE">z</id>
                <id xml:space="preserve" labels="VARIABLE">m</id>
              </sequence>
            </apply>
          </apply>
          <apply>
            <mult />
            <real>2</real>
            <id xml:space="preserve" labels="VARIABLE">m</id>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ES1YCB" actualWidth="260.29100031296412" actualHeight="62.057867054653173" top="422.40000000000009" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="22">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">z</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
            <sequence>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">z</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
            </sequence>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <div />
          <apply>
            <nthRoot />
            <placeholder />
            <apply>
              <plus />
              <apply>
                <neg />
                <parens>
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </parens>
              </apply>
              <real>1</real>
            </apply>
          </apply>
          <apply>
            <nthRoot />
            <placeholder />
            <apply>
              <plus />
              <apply>
                <neg />
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE">z</id>
                  <real>2</real>
                </apply>
              </apply>
              <real>1</real>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

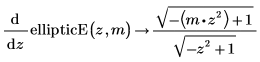
• Erste Ableitungen durch m, n und z des unvollständigen elliptischen Integrals dritter Art:

<region id="ID0EO3YCB" actualWidth="820.6243336462976" actualHeight="62.057867054653173" top="480.00000000000006" left="57.600000000000009" width="820.6243336462976" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="23">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">m</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticPi</id>
            <sequence>
              <id xml:space="preserve">z</id>
              <id xml:space="preserve">n</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
            </sequence>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <minus />
          <apply>
            <div />
            <apply>
              <plus />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <minus />
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                    <real>1</real>
                  </apply>
                </parens>
                <apply>
                  <id xml:space="preserve" labels="FUNCTION">ellipticPi</id>
                  <sequence>
                    <id xml:space="preserve" labels="VARIABLE">z</id>
                    <id xml:space="preserve" labels="VARIABLE">n</id>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </sequence>
                </apply>
              </apply>
              <apply>
                <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
                <sequence>
                  <id xml:space="preserve" labels="VARIABLE">z</id>
                  <id xml:space="preserve" labels="VARIABLE">m</id>
                </sequence>
              </apply>
            </apply>
            <apply>
              <plus />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <real>2</real>
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                    </apply>
                    <real>2</real>
                  </apply>
                </parens>
                <id xml:space="preserve" labels="VARIABLE">n</id>
              </apply>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </apply>
                  <apply>
                    <mult />
                    <real>2</real>
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
              </parens>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <mult />
              <apply>
                <mult />
                <id xml:space="preserve" labels="VARIABLE">m</id>
                <id xml:space="preserve" labels="VARIABLE">z</id>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <real>2</real>
                    </apply>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
            <apply>
              <mult />
              <parens>
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <minus />
                        <apply>
                          <mult />
                          <real>2</real>
                          <id xml:space="preserve" labels="VARIABLE">m</id>
                        </apply>
                        <real>2</real>
                      </apply>
                    </parens>
                    <id xml:space="preserve" labels="VARIABLE">n</id>
                  </apply>
                  <parens>
                    <apply>
                      <minus />
                      <apply>
                        <mult />
                        <real>2</real>
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                      </apply>
                      <apply>
                        <mult />
                        <real>2</real>
                        <apply>
                          <pow />
                          <id xml:space="preserve" labels="VARIABLE">m</id>
                          <real>2</real>
                        </apply>
                      </apply>
                    </apply>
                  </parens>
                </apply>
              </parens>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <parens>
                      <apply>
                        <mult />
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                        <apply>
                          <pow />
                          <id xml:space="preserve" labels="VARIABLE">z</id>
                          <real>2</real>
                        </apply>
                      </apply>
                    </parens>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0E33YCB" actualWidth="1161.1683333333333" actualHeight="57.213600305891042" top="556.80000000000007" left="57.600000000000009" width="1161.1683333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="24">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">n</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticPi</id>
            <sequence>
              <id xml:space="preserve">z</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">n</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
            </sequence>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <minus />
          <apply>
            <neg />
            <apply>
              <div />
              <apply>
                <plus />
                <apply>
                  <mult />
                  <parens>
                    <apply>
                      <minus />
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="VARIABLE">n</id>
                        <real>2</real>
                      </apply>
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                    </apply>
                  </parens>
                  <apply>
                    <id xml:space="preserve" labels="FUNCTION">ellipticPi</id>
                    <sequence>
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <id xml:space="preserve" labels="VARIABLE">n</id>
                      <id xml:space="preserve" labels="VARIABLE">m</id>
                    </sequence>
                  </apply>
                </apply>
                <apply>
                  <plus />
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <minus />
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                        <id xml:space="preserve" labels="VARIABLE">n</id>
                      </apply>
                    </parens>
                    <apply>
                      <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
                      <sequence>
                        <id xml:space="preserve" labels="VARIABLE">z</id>
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                      </sequence>
                    </apply>
                  </apply>
                  <apply>
                    <mult />
                    <id xml:space="preserve" labels="VARIABLE">n</id>
                    <apply>
                      <id xml:space="preserve" labels="FUNCTION">ellipticE</id>
                      <sequence>
                        <id xml:space="preserve" labels="VARIABLE">z</id>
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                      </sequence>
                    </apply>
                  </apply>
                </apply>
              </apply>
              <apply>
                <plus />
                <apply>
                  <minus />
                  <apply>
                    <mult />
                    <real>2</real>
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">n</id>
                      <real>3</real>
                    </apply>
                  </apply>
                  <apply>
                    <mult />
                    <parens>
                      <apply>
                        <plus />
                        <apply>
                          <mult />
                          <real>2</real>
                          <id xml:space="preserve" labels="VARIABLE">m</id>
                        </apply>
                        <real>2</real>
                      </apply>
                    </parens>
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">n</id>
                      <real>2</real>
                    </apply>
                  </apply>
                </apply>
                <apply>
                  <mult />
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </apply>
                  <id xml:space="preserve" labels="VARIABLE">n</id>
                </apply>
              </apply>
            </apply>
          </apply>
          <apply>
            <div />
            <apply>
              <mult />
              <apply>
                <mult />
                <apply>
                  <mult />
                  <id xml:space="preserve" labels="VARIABLE">n</id>
                  <id xml:space="preserve" labels="VARIABLE">z</id>
                </apply>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <parens>
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">m</id>
                          <apply>
                            <pow />
                            <id xml:space="preserve" labels="VARIABLE">z</id>
                            <real>2</real>
                          </apply>
                        </apply>
                      </parens>
                    </apply>
                    <real>1</real>
                  </apply>
                </apply>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <real>2</real>
                    </apply>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
            <apply>
              <plus />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <plus />
                    <apply>
                      <minus />
                      <apply>
                        <mult />
                        <real>2</real>
                        <apply>
                          <pow />
                          <id xml:space="preserve" labels="VARIABLE">n</id>
                          <real>3</real>
                        </apply>
                      </apply>
                      <apply>
                        <mult />
                        <parens>
                          <apply>
                            <plus />
                            <apply>
                              <mult />
                              <real>2</real>
                              <id xml:space="preserve" labels="VARIABLE">m</id>
                            </apply>
                            <real>2</real>
                          </apply>
                        </parens>
                        <apply>
                          <pow />
                          <id xml:space="preserve" labels="VARIABLE">n</id>
                          <real>2</real>
                        </apply>
                      </apply>
                    </apply>
                    <apply>
                      <mult />
                      <apply>
                        <mult />
                        <real>2</real>
                        <id xml:space="preserve" labels="VARIABLE">m</id>
                      </apply>
                      <id xml:space="preserve" labels="VARIABLE">n</id>
                    </apply>
                  </apply>
                </parens>
                <apply>
                  <pow />
                  <id xml:space="preserve" labels="VARIABLE">z</id>
                  <real>2</real>
                </apply>
              </apply>
              <parens>
                <apply>
                  <minus />
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <parens>
                        <apply>
                          <plus />
                          <apply>
                            <mult />
                            <real>2</real>
                            <id xml:space="preserve" labels="VARIABLE">m</id>
                          </apply>
                          <real>2</real>
                        </apply>
                      </parens>
                      <id xml:space="preserve" labels="VARIABLE">n</id>
                    </apply>
                    <apply>
                      <mult />
                      <real>2</real>
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="VARIABLE">n</id>
                        <real>2</real>
                      </apply>
                    </apply>
                  </apply>
                  <apply>
                    <mult />
                    <real>2</real>
                    <id xml:space="preserve" labels="VARIABLE">m</id>
                  </apply>
                </apply>
              </parens>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0EK4YCB" actualWidth="443.1703339592616" actualHeight="58.587600193993254" top="614.40000000000009" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="25">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <derivative />
        <lambda>
          <boundVars>
            <id xml:space="preserve">z</id>
          </boundVars>
          <apply>
            <id xml:space="preserve" labels="FUNCTION">ellipticPi</id>
            <sequence>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">z</id>
              <id xml:space="preserve">n</id>
              <id xml:space="preserve" labels="VARIABLE" label-is-contextual="true">m</id>
            </sequence>
          </apply>
        </lambda>
        <degree>
          <placeholder />
        </degree>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <apply>
          <neg />
          <apply>
            <div />
            <real>1</real>
            <apply>
              <mult />
              <apply>
                <mult />
                <parens>
                  <apply>
                    <minus />
                    <apply>
                      <mult />
                      <id xml:space="preserve" labels="VARIABLE">n</id>
                      <apply>
                        <pow />
                        <id xml:space="preserve" labels="VARIABLE">z</id>
                        <real>2</real>
                      </apply>
                    </apply>
                    <real>1</real>
                  </apply>
                </parens>
                <apply>
                  <nthRoot />
                  <placeholder />
                  <apply>
                    <plus />
                    <apply>
                      <neg />
                      <parens>
                        <apply>
                          <mult />
                          <id xml:space="preserve" labels="VARIABLE">m</id>
                          <apply>
                            <pow />
                            <id xml:space="preserve" labels="VARIABLE">z</id>
                            <real>2</real>
                          </apply>
                        </apply>
                      </parens>
                    </apply>
                    <real>1</real>
                  </apply>
                </apply>
              </apply>
              <apply>
                <nthRoot />
                <placeholder />
                <apply>
                  <plus />
                  <apply>
                    <neg />
                    <apply>
                      <pow />
                      <id xml:space="preserve" labels="VARIABLE">z</id>
                      <real>2</real>
                    </apply>
                  </apply>
                  <real>1</real>
                </apply>
              </apply>
            </apply>
          </apply>
        </apply>
      </symResult>
    </symEval>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

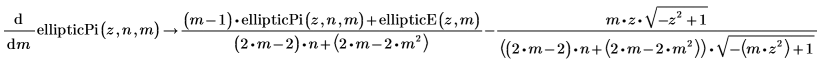
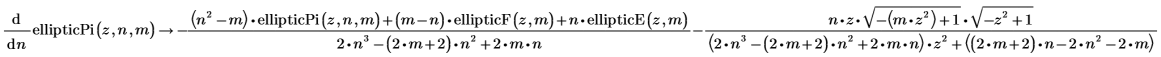
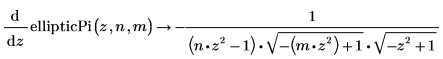
Elliptische Integralfunktionen numerisch auswerten

• Verwenden Sie das Schlüsselwort assume.

<region id="ID0EL6YCB" actualWidth="273.84000000000003" actualHeight="51.158666666666669" top="710.40000000000009" left="57.600000000000009" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="26">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION">ellipticF</id>
        <sequence>
          <id xml:space="preserve">z</id>
          <id xml:space="preserve">m</id>
        </sequence>
      </apply>
      <command>
        <sequence>
          <sequence>
            <id xml:space="preserve">assume</id>
            <apply>
              <equal />
              <id xml:space="preserve">z</id>
              <real>1</real>
            </apply>
          </sequence>
          <apply>
            <equal />
            <id xml:space="preserve">m</id>
            <real>0</real>
          </apply>
        </sequence>
      </command>
      <symResult>
        <apply>
          <div />
          <id xml:space="preserve" labels="CONSTANT">π</id>
          <real>2</real>
        </apply>
      </symResult>
    </symEval>
  </math>
</region>

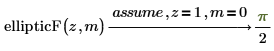
Sie können auch die Funktionsargumente festlegen.

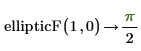
Berechnen Sie den Grenzwert von ellipticF bei m Annäherungen an 0:

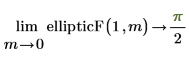
• Verwenden Sie das Schlüsselwort float.

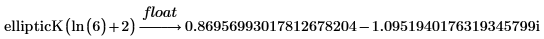
• ellipticK hat einen Singularitätspunkt bei m=1. Für m>1 sind die Ergebnisse komplex:

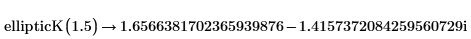
• Berechnen Sie das ellipticK eines Vektors.

<region id="ID0E3FZCB" actualWidth="511.88333333333333" actualHeight="81.4" top="1036.8000000000002" left="76.800000000000011" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="31">
    <symEval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id xml:space="preserve" labels="FUNCTION">ellipticK</id>
        <matrix rows="4" cols="1">
          <real>-0.5</real>
          <real>0.5</real>
          <real>1</real>
          <real>1.5</real>
        </matrix>
      </apply>
      <command>
        <placeholder />
      </command>
      <symResult>
        <matrix rows="4" cols="1">
          <real>1.415737208425956295</real>
          <real>1.8540746773013719184</real>
          <id xml:space="preserve" labels="CONSTANT">∞</id>
          <apply>
            <minus />
            <real>1.6566381702365939876</real>
            <imag symbol="i">1.4157372084259560729</imag>
          </apply>
        </matrix>
      </symResult>
    </symEval>
  </math>
</region>

Zugehörige Themen

Elliptische Integralfunktionen

Symbolische Funktionen

War dies hilfreich?