Elliptische Integralfunktionen
Elliptische Integralfunktionen sind eine Gruppe von Integralfunktionen der folgenden Form:
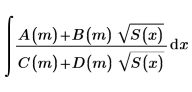
A(m), B(m), C(m) und D(m) sind Polynome und S(x) ist ein Polynom mit Grad 3 oder 4. Elliptische Integralfunktionen sind nützlich bei vielen Rechenproblemen, einschließlich Elektromagnetismus und Gravitation.
Elliptische Integralfunktionen können in vollständiger oder unvollständiger Form verwendet werden. Die vollständige Form berechnet das Integral von 0 bis 1. Die unvollständige Form berechnet das Integral von 0 bis zu einer Variablen z. Sie können die folgenden elliptischen Integralfunktionen in Mathcad verwenden:
• ellipticK – vollständiges elliptisches Integral erster Art:
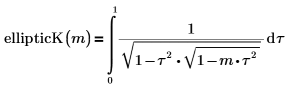
• ellipticF – unvollständiges elliptisches Integral erster Art:
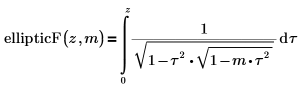
• ellipticE – vollständiges elliptisches Integral zweiter Art:
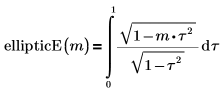
• ellipticE – unvollständiges elliptisches Integral zweiter Art:
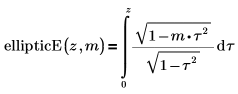
• ellipticPi – vollständiges elliptisches Integral dritter Art:
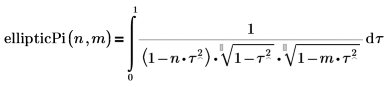
• ellipticPi – unvollständiges elliptisches Integral dritter Art:
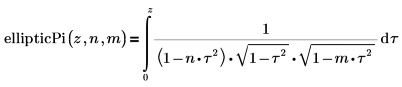
Sehen Sie sich das Verhalten der Funktion ellipticK zwischen 0 und 10 an. Das Ergebnis ist eine reelle Zahl, wenn es 0<m<1 ist, und eine komplexe Zahl, wenn es m>1 ist.
Die grüne Kurve stellt die reellen Ergebnisse dar, und die orangefarbene Kurve stellt die komplexen Ergebnisse dar.

Argumente
• m ist ein Skalar oder ein Vektor.
• n und z sind Skalare.