Beispiel: Eigenvektoren und Eigenwerte
Verwenden Sie die Funktionen eigenvals, eigenvecs und eigenvec, um die Eigenwerte und die Eigenvektoren einer reellen oder komplexen Matrix zu ermitteln. Überprüfen Sie die Theorie, dass für die quadratische Matrix M ein Vektor M, der ungleich null ist, dem Eigenvektor von v entspricht, wenn eine Zahl λ gefunden wird, sodass Folgendes gilt:
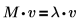
1. Definieren Sie eine quadratische Eingabematrix.
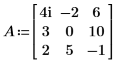
2. Rufen Sie die Funktionen eigenvals und eigenvecs auf, um die Eigenwerte und die Eigenvektoren von Matrix A zu ermitteln.
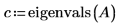
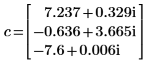
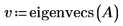

Die erste Spalte von v ist der Eigenvektor, der dem ersten Element von c entspricht. Analog ist die zweite Spalte von v der Eigenvektor, der dem zweiten Element von c entspricht usw.
3. Definieren Sie v1 als ersten Eigenvektor und c1 als ersten Eigenwert von A. Vergleichen Sie A x v1 mit c1 x v1.
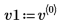
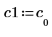
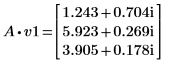 | 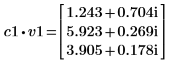 |
4. Definieren Sie v2 als ersten Eigenvektor und c2 als ersten Eigenwert von A. Vergleichen Sie A x v2 mit c2 x v2.
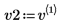
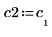
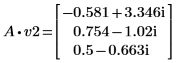 | 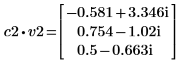 |
5. Definieren Sie v3 als ersten Eigenvektor und c3 als ersten Eigenwert von A. Vergleichen Sie A x v3 mit c3 x v3.
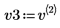
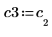
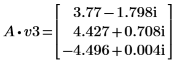 | 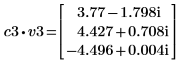 |
6. Rufen Sie die Funktion eigenvec auf, um einen Eigenvektor für einen bestimmten Eigenwert zurückzugeben.
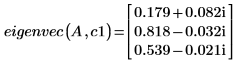

Die Ergebnisse, die von eigenvec und eigenvecs zurückgegeben werden, sind nicht unbedingt identisch, stellen jedoch gültige Lösungen dar. Ein Eigenvektor ist nicht eindeutig. Er steht über einen Skalierungsfaktor mit anderen Eigenvektoren in Beziehung. Für einen bestimmten Eigenwert ist eine unendliche Anzahl an Eigenvektoren verfügbar.