Beispiel: Kombinationen und Permutationen
Verwenden Sie die Funktionen combin und permut, um Untermengen von Elementen aufzuzählen. Die Reihenfolge der Elemente ist signifikant n Permutationen, aber nicht in Kombinationen.
1. Legen Sie die Anzahl der Elemente und die Anzahl der Elemente in jeder Untermenge fest:
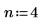
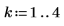
2. Wenden Sie die Funktion combin an, um die Anzahl der Kombinationen zu berechnen:
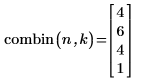
Bei vier Elementen gibt es vier Möglichkeiten, jeweils ein Element zu gruppieren, sechs Möglichkeiten, jeweils zwei Elemente zu gruppieren, vier Möglichkeiten, jeweils drei Elemente zu gruppieren und eine Möglichkeit, jeweils vier Elemente zu gruppieren.
3. Angenommen, die Buchstaben A, B, C und D sind gegeben. Listen Sie die vier Kombinationen von einem Buchstaben pro Satz auf:
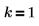 | A, B, C, D |
4. Listen Sie die sechs Kombinationen von zwei Buchstaben pro Satz auf:
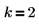 | AB, AC, AD, BC, BD, CD |
Die Sätze BA, CA, DA, CB, DB, DC enthalten die gleichen Buchstaben wie AB, AC usw. und werden daher nicht als verschiedene Kombinationen gezählt.
5. Wenden Sie die Funktion permut an, um die Anzahl der Permutationen zu berechnen:
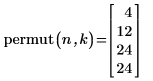
6. Listen Sie die 12 Permutationen bei zwei Buchstaben pro Satz auf:
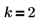 | AB, AC, AD, BC, BD, CD |
BA, CA, DA, CB, DB, DC |
Die Sätze AB und BA werden als verschiedene Permutationen von A und B behandelt.
7. Listet die 24 Permutationen von drei Buchstaben pro Satz auf:
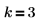 | ABC, ACB, ABD, ADB, ACD, ADC |
BAC, BCA, BAD, BDA, BCD, BDC | |
CAB, CBA, CAD, CDA, CBD, CDB | |
DAB, DBA, DBC, DCB, DAC, DCA |