Beispiel: Binomialverteilungen und negative Binomialverteilungen

Funktionen > Statistik > Wahrscheinlichkeitsverteilungen > Beispiel: Binomialverteilungen und negative Binomialverteilungen

Binomialverteilungen

1. Verwenden Sie die Funktion dbinom, um die Wahrscheinlichkeitsdichte für den Wert k zu berechnen.

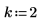
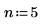
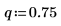
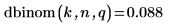
2. Verwenden Sie die Funktion pbinom, um die kumulative Wahrscheinlichkeitsverteilung für den Wert k zu berechnen.

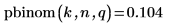
3. Verwenden Sie die Funktion qbinom, um die umgekehrte kumulative Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeit p zu berechnen.

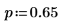
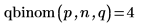
4. Verwenden Sie die Funktion rbinom, um einen Vektor von m Zufallszahlen zu erstellen, die die Binomialverteilung aufweisen.

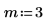
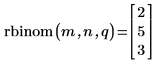
Die Neuberechnung des Arbeitsblatts bewirkt, dass die Funktion rbinom einen neuen Satz von Zufallszahlen zurückgibt.

Negative Binomialverteilungen

1. Verwenden Sie die Funktion dnbinom, um die Wahrscheinlichkeitsdichte für den Wert k zu berechnen.

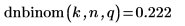
2. Verwenden Sie die Funktion pnbinom, um die kumulative Wahrscheinlichkeitsverteilung für den Wert k zu berechnen.

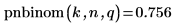
3. Verwenden Sie die Funktion qnbinom, um die umgekehrte kumulative Wahrscheinlichkeitsverteilung für die Wahrscheinlichkeit p zu berechnen.

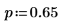
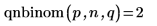
4. Verwenden Sie die Funktion rnbinom, um einen Vektor von m Zufallszahlen zu erstellen, die die Binomialverteilung aufweisen.

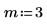
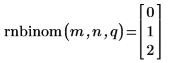
Die Neuberechnung des Arbeitsblatts bewirkt, dass die Funktion rnbinom einen neuen Satz von Zufallszahlen zurückgibt.

5. Plotten und vergleichen Sie die Funktion rbinom mit der Funktion rnbinom, wobei Sie dieselben Parameter verwenden.

<region id="ID0EEWHCB" top="1670.4000000000003" left="38.400000000000006" height="102.15200000000002" width="274.45333333333338" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="97">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">Pn</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">pnbinom</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">k</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">n</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">q</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

<region id="ID0ESWHCB" top="1747.2000000000003" left="38.400000000000006" height="288" width="576.39999999999964" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="99">
          <traceStyle color="#FF068149" symbol="filledStar" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="100">
          <traceStyle color="#FFED1D2F" symbol="filledRectangle" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="476.4" height="230.4" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="4">
          <axisLine position="origin" positionticmark="0" legendWidth="57.5433333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math resultRef="103">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">i</id>
              </math>
              <math resultRef="104">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="102">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="1">
          <axisLine position="origin" positionticmark="0" legendWidth="75.2533333333333" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers>
            <marker resultRef="105" display="true" color="#FF068149" line-style="Dash" value="0.50000000000000344">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">P</id>
                <real>2</real>
              </apply>
            </marker>
            <marker resultRef="107" display="true" color="#FFED1D2F" line-style="Dash" value="0.22656250000000039">
              <apply xmlns="http://schemas.mathsoft.com/math50">
                <indexer />
                <id xml:space="preserve">Pn</id>
                <real>2</real>
              </apply>
            </marker>
          </markers>
          <plotEquations>
            <plotEquation>
              <math resultRef="109">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id xml:space="preserve">P</id>
                  <id xml:space="preserve">i</id>
                </apply>
              </math>
              <math resultRef="110">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="111">
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <indexer />
                  <id xml:space="preserve">Pn</id>
                  <id xml:space="preserve">i</id>
                </apply>
              </math>
              <math resultRef="112">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

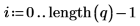
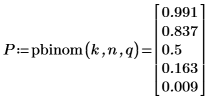
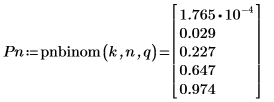
Die beiden Funktionen sind nicht das Negative der jeweils anderen.

Zugehörige Themen

Binomische Verteilung

Negative Binomialverteilung

War dies hilfreich?