Logarithmische Integralfunktionen
Die logarithmische Integralfunktion li(x) ist eine spezielle Funktion zum Lösen bestimmter Probleme in der Physik und Zahlentheorie. Sie liefert eine sehr gute Näherung der Primzahlfunktion, mit der die Anzahl der Primzahlen kleiner oder gleich einem gegebenen Wert ermittelt wird.
• li(x) – Gibt das logarithmische Integral von x zurück, das für alle positiven reellen Zahlen definiert ist, wobei x ≠ 1 ist.

Das Integral für x >1 wird als der Cauchy-Hauptwert interpretiert.
Die Funktion 1/ln(x) hat eine Singularität bei x =1:
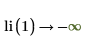
• Bei x >0 ist die logarithmische Integralfunktion wie folgt mit der Exponentiellen Integralfunktion verbunden:
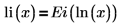
Li(x) – Gibt die logarithmische Versatzintegralfunktion von x zurück, die wie folgt definiert ist:
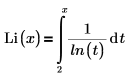
Argumente
• x ist ein reeller oder komplexer Skalar oder ein Vektor von reellen oder komplexen Skalaren.
Zusätzliche Informationen
• Sie können die logarithmische Integralfunktion und die logarithmische Versatzintegralfunktion nur symbolisch auswerten.