具有無限限制之積分數值計算的非整合情況
本主題提供了以數字形式使用一個或兩個無限整合限制計算積分時,兩種非整合誤差情況的因應措施。
若要說明這兩種情況,請定義一個平均值 μ 和一個標準差 σ。
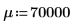
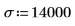
案例 I:具有一個無限整合限制的積分
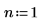
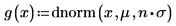
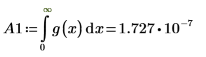
n=1 時,範圍 [0, ∞] 內的 g(x) 積分計算不會傳回錯誤,但會傳回一個非常小的值。
案例 I 的因應措施
將 n 的值增加到 n=2 並重新計算積分。
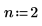
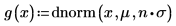
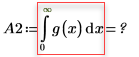
因為計算並未與求解整合,將 n 的值增加到 n=2,會導致錯誤。
作為一種因應措施,將變數 T 設定為與 g(x) 的結尾接近的值,然後將單一積分分割為二:一個是涵蓋範圍 [0, T] 的值,另一個是涵蓋範圍 [T, ∞] 的值。
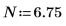 | 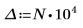 |
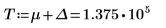 |
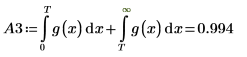
n=1 或 n=2 時,分割積分 A3 會傳回一個適當的答案。繪製 g(x) 並新增垂直標記 T,以查看 g(x) 結尾的接近程度。
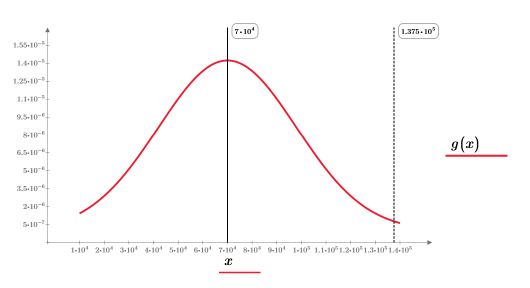
因為垂直標記靠近 g(x) 的結尾,繪圖會顯示變數 T。
案例 II:具有兩個無限整合限制的積分
將乘數變數 n 設定為1,然後計算範圍 [-∞, ∞] 內 g(x) 的積分。
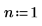
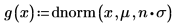
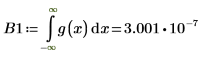
n=1 時,範圍 [-∞, ∞] 內的 g(x) 積分計算不會傳回錯誤,但會傳回一個非常小的值。
案例 II 的因應措施
作為一種因應措施,將變數 T1 與 T2 設定為接近 g(x) 的頭部與結尾的值,然後將單一積分分割為三個積分:一個是涵蓋範圍 [-∞, T1] 的值,一個是涵蓋範圍 [T1, T2] 的值,另一個是涵蓋範圍 [T2, ∞] 的值。
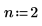
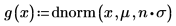
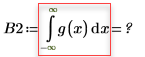
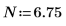 | 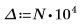 |
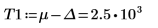 | 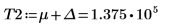 |
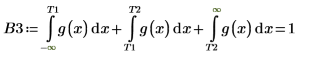
n=1 或 n=2 時,分割積分會傳回一個適當的答案。繪製 g(x) 並新增垂直標記 T1 與 T2,並查看它們與 g(x) 的頭部和尾部之間的接近程度。
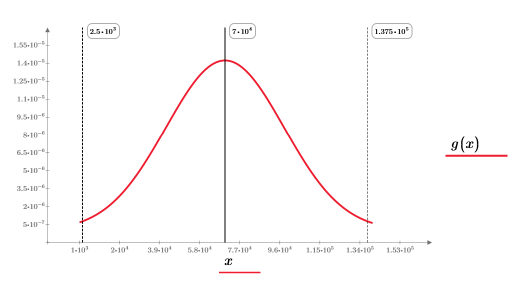
查看與結論
使用相同的平均值但兩個不同的標準差值,繪製內建機率密度函數 dnorm。
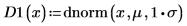
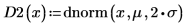
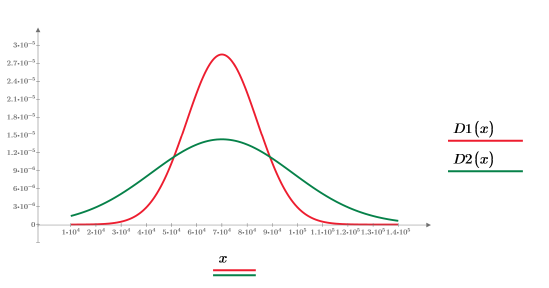
繪圖會顯示:
• 較小的標準差值會導致曲線下的區域主體更靠近平均值。在此情況下,數值計算會整合,但會傳回錯誤答案。
• 較大的標準差值會導致曲線下的區域主體遠離平均值。在此情況下,數值計算無法整合。
在這兩種情況下,分割積分可確保計算整合並傳回正確答案。