範例:殘差分析
計算數據集的殘差,以檢查集合是否為線性分佈。使用遞歸模型進行預測之前,請先檢查是否符合線性模型假設:
• 誤差必須不相關。
• 至於 X 所有的指定值,誤差應為常態分佈,且有零均數及固定變異數。
標準化殘差
若要轉譯殘差的相關量值,可使其標準化。殘差必須除以誤差標準差的估值。
1. 定義下列數據集:
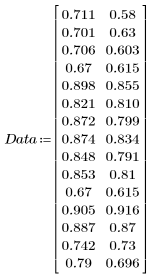
2. 繪製數據集。
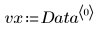
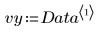
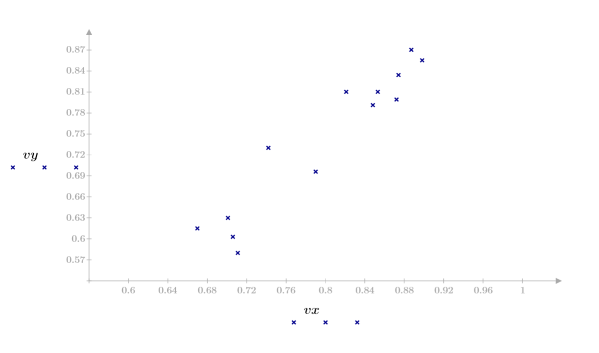
數據似乎為線性數據。近似於 1 的相關係數可證實:
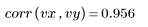
3. 定義最佳擬合線:
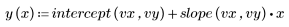
4. 將量測值減去擬合值。
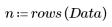
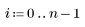
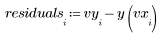
5. 將殘差除以估值的標準誤差。
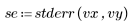
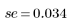
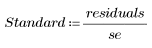
T 化殘差
T 化殘差或調整過的標準化殘差,是另一種常用的標準誤差預測方法。此估值會調整 x 各值及 x 均數間的距離。
1. 計算值與均數之間的距離。
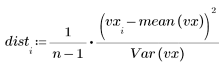
2. 定義按各殘差組合的標準差。

3. 定義 T 化殘差:
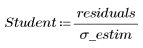
T 化殘差比標準化殘差更精確,因為它們計入誤差變異數中所有點對點的差異。不過,值中的殘差通常都很接近:
 |  |
4. 呼叫 polyfitstat。顯示包含 T 化殘差的觀測診斷子矩陣。
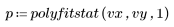
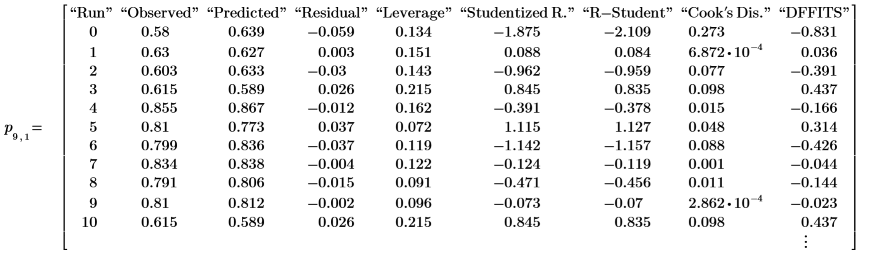
檢查是否有線性
檢查 Data 集合是否為線性相關。使用具有曲線相關的隨機樣本建立反例。若數據為線性相關,且誤差為常態分佈,則散佈圖無任何可識別的圖樣。點會隨機散佈在假設誤差均數零的周圍。
1. 對照 x 值與預測的 y 值,繪製殘差。
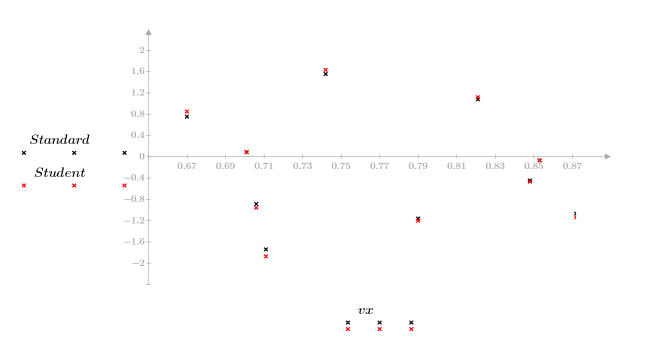
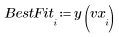
缺少殘差圖樣表示數據屬於線性相關。
2. 產生具有二次關係的隨機樣本點。
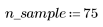
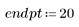
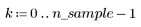
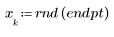
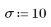
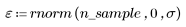
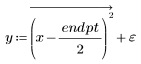
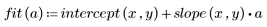
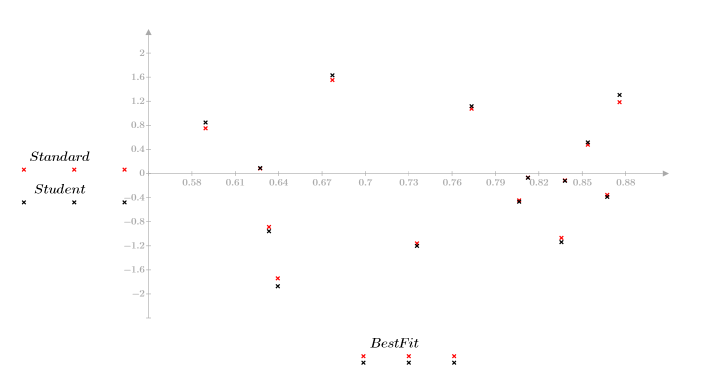
3. 繪製殘差的相對量值。
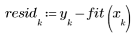
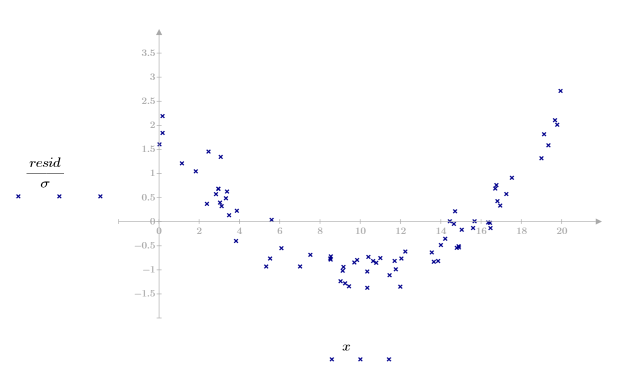
數據中的二次圖樣反映在殘差散佈圖中。此數據非線性相關。
檢查是否有誤差變異數
在 Data 集合中未檢測到任何誤差變異數模式。建立數據顯示線性,但誤差變異數非常態分佈的反例,以及顯示由左向右遞增或遞減散佈的殘差散佈圖。
1. 產生從左至右散佈得愈來愈多的隨機樣本點。
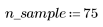
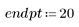
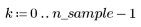
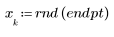
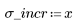
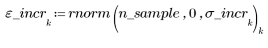
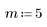
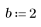
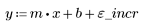
2. 計算最佳擬合線。繪製隨機數據集與擬合函數。
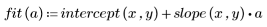
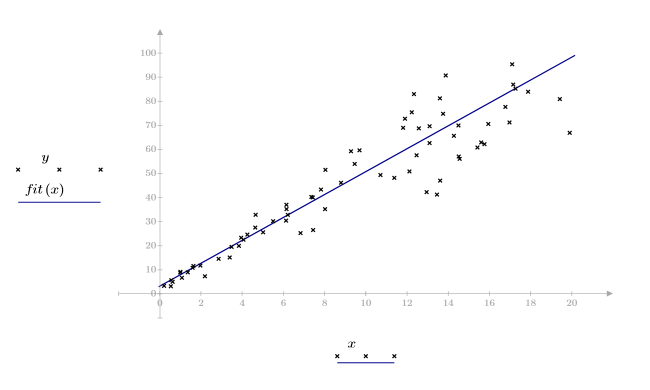
相關係數近似於 1 表示數據為線性相關:
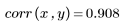
3. 繪製殘差的相對量值。
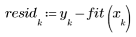
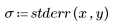
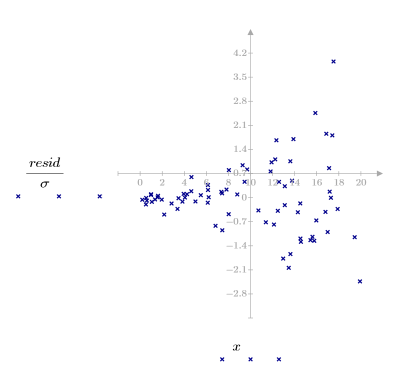
殘差的散佈圖不會出現隨機分佈。殘差圖中的點由左向右散佈得愈來愈多。
檢查是否有誤差相關運算
您可使用 Durbin-Watson 統計,檢查線性遞歸模型中的相鄰誤差項是否相關。
計算 Data 集合的 Durbin-Watson 統計:
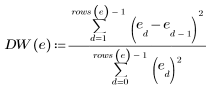
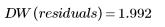
Durbin-Watson 的值範圍從 0 到 4。若鄰項不相關,則 Durbin-Watson 值近似於 2。Durbin-Watson 值小於 2 表示正相鄰相關,值大於 2 表示負相關。
Durbin-Watson 統計係用於計算最小平方 B 雲規線。可惜的是,Durbin-Watson 統計無法檢測階數較高 (非相鄰) 的係數。若相鄰誤差間沒有相關性,則這些相關性類型即不會常出現。
Durbin-Watson 統計是 polyfitstat 傳回的統計之一:
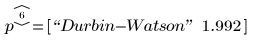
檢查是否有常態性
建立標準化殘差的常態圖,以檢查 Data 集合是否為常態分佈。
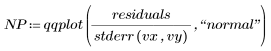
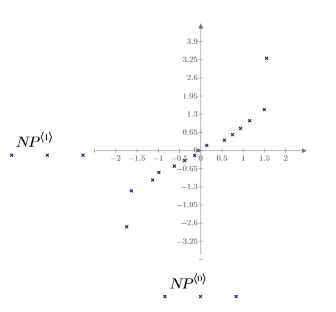
常態圖類似於直線。因此誤差近似於常態分佈。因為常態圖會隨其他假設違反波動,例如當誤差變異數不相等時,所以最好是最後再檢查常態性。