多變量多項式遞歸的統計
• polyfitstat(X, Y, n/"terms"/M, [conf]) - 傳回多項式遞歸模型將矩陣 Y 中記錄的結果擬合至矩陣 X 中的統計數據。您可依多項式遞歸方程式的多項式冪次 n 或依其在字串 “terms” 或矩陣 M 中指定的項數,定義多項式遞歸方程式。若不想在擬合多項式中包括截距,請使用矩陣 M。使用選用引數 conf 可指定信心區間,而非使用預設值 95%。
polyfitstat 傳回之矩陣的第二欄包含下列元素:
|
Row
|
描述
|
|---|---|
|
1
|
Y 的標準差
|
|
2, 3, 4
|
R2、調整後的 R2 與預測的 R2
|
|
5
|
PRESS - 平方的預測誤差總和 (可用於調整殘差)
|
|
6
|
適用於自相關的 Durbin-Watson 測試統計
|
|
7
|
如 polyfitc 所傳回的遞歸係數矩陣
|
|
8
|
變數分析(ANOVA) 的矩陣,適用於所含之欄等同於 anova 所傳回的結果表格,且包含以下數列的遞歸模型:
• 遞歸 - 小計,後續會細分至各項 (截距除外)
• 殘差 (誤差) - 小計,後續會細分至「缺適性」誤差與「純實驗性」誤差之間
• 遞歸模型的總計
|
|
9
|
含有下列各欄的診斷矩陣:
1. 每次執行或每個數據點的編號
2. 每次執行或每個數據點的觀測結果
3. 遞歸模型根據調查所做的預測結果
4. 殘差 - 觀測結果與預測結果之間的差分
5. 力距 - 觀測結果與所有觀測結果中心點之間的距離量值
6. T-測試殘差 - 除以觀測結果的變異數之殘差
7. R-student - 除以移除觀測結果後的數據集所產生的變異數,所得之殘差
8. 庫克距離 - 觀測結果對其餘所有數據點的影響量值
9. DFFITS - 遞歸模型根據納入觀測結果的數據集所預測的結果,與其他移除觀測結果的模型所預測的結果之間的差異
|
引數
• X 是設計矩陣或矩陣,其中每一欄各代表一個自變數。X 的每一欄都必須具有相容的單位。
• Y 是量測或模擬結果的向量或矩陣,其中每一列包含 X 中所定義之每次執行或每個數據點的結果。若每一列所含的複製數目不一定相同,則必須以 NaN 填補 Y 的空白元素。Y 的元素必須具有相容的單位。
• n 是指定多項式階數的整數。它必須小於數據點的總數:1 ≤ n ≤ length(Y) − 1。否則,問題會受限為沒有唯一的解。
• “terms” 是指定要包括在多項式遞歸中之項數 (或係數與相互作用) 的字串。"A B AB AA BB" 表示多項式包含下列項數:
c0 + c1 ∙ A + c2 ∙ B + c3 ∙ A ∙ B + c4 ∙ A2 + c5 ∙ B2
您可以使用空格、逗號、冒號或分號作為分隔符號。
• M 是指定多項式的矩陣,其第一欄中含有係數的估值,而剩餘欄中則含有每個項數的自變數次方。針對上述多項式,如下定義 M:
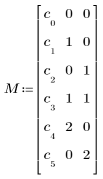
• conf (選用) 是所需的信心限制,並以介於 0 到 1 (含) 之間的數字所表示的百分比指定。根據預設,conf = 0.95 表示 95% 的信心區間。