範例:有理函數遞歸 2
rationalfitnp - 無極點
使用 rationalfit 及 rationalfitnp 函數執行有理函數遞歸。當您使用 rationalfitnp 函數而不使用 rationalfit 函數時,會檢查傳統最小平方問題的解在擬合區間內是否有分母的根。若無任何極點,即會傳回產生的擬合。若有極點,則非線性最佳化問題會加入其他條件約束。
1. 略微修改 x 的反函數,以定義數據集。
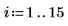
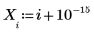
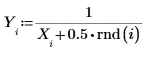
2. 指定有理函數的分子及分母順序。
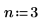
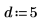
擬合函數有下列格式:
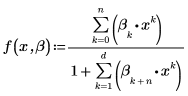
3. 定義標準差的信心限制及向量。
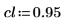
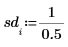
4. 呼叫 rationalfit 與 rationalfitnp 函數。
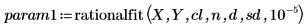 | 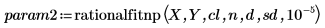 |
 |  |
param1 與 param2 的第一欄為參數,其餘欄則為前文中所定義之信心限制之各參數的上下邊界。
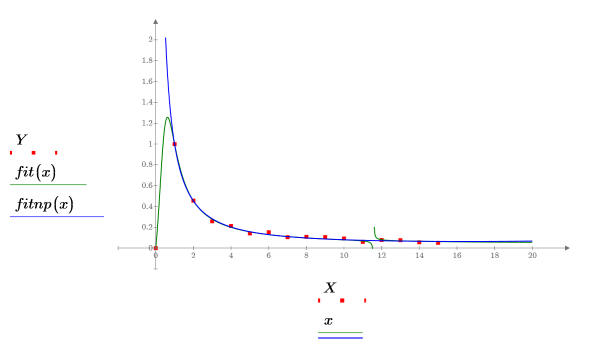
5. 繪製數據集與兩條遞歸曲線。
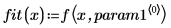
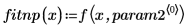
rationalfitnp 函數會移除極點。其分母多項式以下列格式計算:
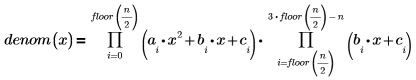
若要避免極點,必須加入下列條件約束:
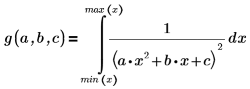
 | 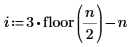 |
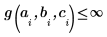 | 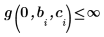 |
LeastSquaresFit
比較 rationalfitnp 及 LeastSquaresFit 傳回的擬合曲線。LeastSquaresFit 函數與 rationalfitnp 執行相同的演算法,但它需要估值與參數的信心限制。當您要常數項在分子而不在分母時,可以執行此作業。
1. 定義擬合函數。
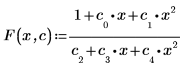
2. 定義參數的估值。
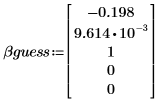
3. 定義參數的上下邊界條件。

4. 呼叫 LeastSquaresFit 函數。
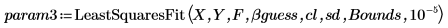
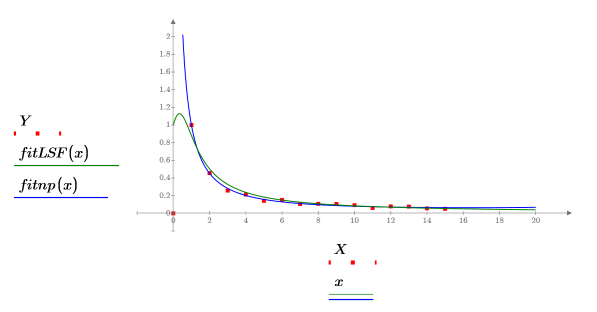
5. 繪製數據集、rationalfitnp 傳回的擬合曲線及 LeastSquaresFit 函數。
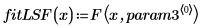
在執行有理函數擬合前,所有讓數據偏向直線的濾波或數據轉換方法,都會在 rational 函數中加入可觀的收歛速度,並可能產生除去不需要之極點的額外好處。 |