範例：QR 矩陣因式分解

函數 > 向量與矩陣 > 矩陣因式分解 > 範例：QR 矩陣因式分解

範例：QR 矩陣因式分解

使用 QR 函數執行 QR 矩陣因式分解。

• 為避免在執行布林比較時發生邏輯不符的情況，請啟用「計算選項」下拉式清單中的「近似等式」。

• 此範例使用複數矩陣作為輸入，但此函數也接受實數矩陣作為輸入。

使用樞軸的 QR 因式分解

1. 定義維度 m x n 的實數矩陣 M1，例如 m > n。

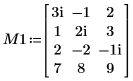
2. 設定引數 p 控制樞軸的啟用/停用。

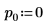
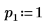
3. 使用 QR 函數執行矩陣 M1 的 QR 矩陣因式分解。

預設函數 QR(M1) 等同於 QR(M,1).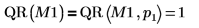

4. 顯示 M1 x P1 = Q1 x R1。

<region id="ID0EWRBFB" actualWidth="167.83666666666665" actualHeight="81.4" top="1209.6000000000001" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="16"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P1</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EESBFB" actualWidth="165.74" actualHeight="81.4" top="1209.6000000000001" left="211.20000000000005" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="18"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R1</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EXSBFB" actualWidth="153.23666666666668" actualHeight="25.6" top="1286.4" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="20"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P1</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q1</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R1</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
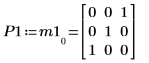
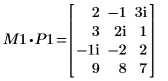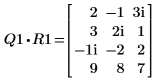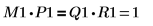此關係在邏輯上為真。

5. 使用 submatrix 函數萃取矩陣 M2，例如 m < n，然後套用 QR 函數。

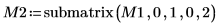
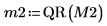
6. 顯示 M2 x P2 = Q2 x R2。

<region id="ID0EGZBFB" actualWidth="69.890000000000015" actualHeight="36.800000000000004" top="1516.8000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="26"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EUZBFB" actualWidth="71.38666666666667" actualHeight="36.800000000000004" top="1516.8000000000002" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="28"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">Q2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EC1BFB" actualWidth="70.816666666666677" actualHeight="36.800000000000004" top="1516.8000000000002" left="230.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="30"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">R2</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m2</id> <real>2</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EV1BFB" actualWidth="153.23666666666668" actualHeight="25.6" top="1555.2000000000003" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="32"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M2</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P2</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q2</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R2</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
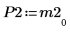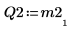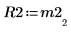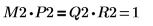此關係在邏輯上為真。

7. 使用 submatrix 函數萃取矩陣 M3，例如 m = n，然後套用 QR 函數。

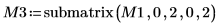
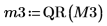
8. 顯示 M3 x P3 = Q3 x R3。

<region id="ID0E3ACFB" actualWidth="69.890000000000015" actualHeight="36.800000000000004" top="1785.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="38"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">P3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EKBCFB" actualWidth="71.38666666666667" actualHeight="36.800000000000004" top="1785.6000000000004" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="40"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">Q3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EYBCFB" actualWidth="70.816666666666677" actualHeight="36.800000000000004" top="1785.6000000000004" left="230.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="42"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">R3</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m3</id> <real>2</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0ELCCFB" actualWidth="153.23666666666668" actualHeight="25.6" top="1824.0000000000002" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="44"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M3</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">P3</id> </apply> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q3</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R3</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
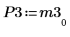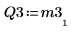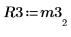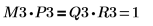此關係在邏輯上為真。

使用無樞軸的 QR 因式分解

1. 停用樞軸，然後將 QR 函數套用至矩陣 M1 (m > n)。

2. 顯示 M1 = Q10 x R10。

<region id="ID0E6ICFB" actualWidth="140.69333333333333" actualHeight="81.4" top="2380.8" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="52"> <eval xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ENJCFB" actualWidth="170.95" actualHeight="81.4" top="2380.8" left="211.20000000000005" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="54"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q10</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R10</id> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EAKCFB" actualWidth="142.05333333333334" actualHeight="25.6" top="2457.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="56"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M1</id> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q10</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R10</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
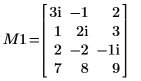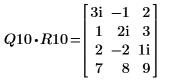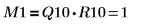此關係在邏輯上為真。

3. 停用樞軸，然後將 QR 函數套用至矩陣 M2 (m < n)。

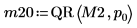
4. 顯示 M2 = Q20 x R20。

<region id="ID0EFPCFB" actualWidth="87.346666666666664" actualHeight="36.800000000000004" top="2649.6000000000004" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="60"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">Q20</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m20</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0ETPCFB" actualWidth="86.776666666666671" actualHeight="36.800000000000004" top="2649.6000000000004" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="62"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">R20</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m20</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0EGQCFB" actualWidth="142.05333333333334" actualHeight="25.6" top="2688.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="64"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M2</id> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q20</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R20</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
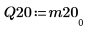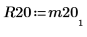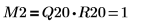此關係在邏輯上為真。

5. 停用樞軸，然後將 QR 函數套用至矩陣 M3 (m = n)。

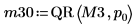
6. 顯示 M3 = Q30 x R30。

<region id="ID0EKVCFB" actualWidth="87.346666666666664" actualHeight="36.800000000000004" top="2880.0000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="68"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">Q30</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m30</id> <real>0</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>	<region id="ID0EYVCFB" actualWidth="86.776666666666671" actualHeight="36.800000000000004" top="2880.0000000000005" left="134.40000000000003" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="70"> <define xmlns="http://schemas.mathsoft.com/math50"> <id labels="VARIABLE" xml:space="preserve">R30</id> <apply> <indexer /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m30</id> <real>1</real> </apply> </define> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
<region id="ID0ELWCFB" actualWidth="142.05333333333334" actualHeight="25.6" top="2918.4000000000005" left="38.400000000000006" xmlns="http://schemas.mathsoft.com/worksheet50"> <math resultRef="72"> <eval xmlns="http://schemas.mathsoft.com/math50"> <apply> <equal /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">M3</id> <apply> <mult /> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Q30</id> <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">R30</id> </apply> </apply> <unitOverride> <placeholder /> </unitOverride> </eval> <resultFormat> <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" /> </resultFormat> </math> </region>
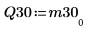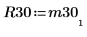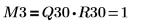此關係在邏輯上為真。

相關主題

關於矩陣因式分解函數

這是否有幫助?