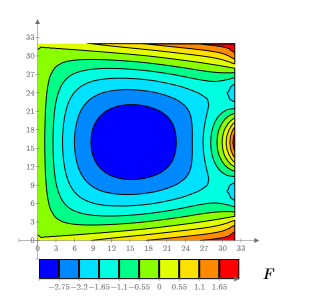
範例:方形平板上的熱流 - II
使用偏微分方程式求解器 relax 求解方形平板的穩態溫度分佈。
求解普松方程式
求解熱方程式,其中來源函數值已知,且邊界條件為非零。
|
|
relax 函數是以完全不同的解法為基礎,因此需要一組不同的引數。
|
1. 定義五個包含拉普拉斯近似係數的方形矩陣 a、b、c、d 及 e:
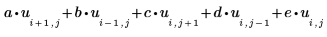
這些陣列可以是您指定的任何大小。陣列愈大,解的網格愈細密。 |
2. 定義方形平板的維度:
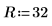
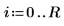
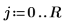
3. 定義係數:
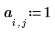
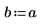
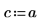
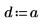
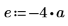
4. 定義固定來源的強度與位置。
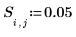
5. 定義大小等於格點大小的方形矩陣 f,以包含函數 F(x,y) 的已知邊界值及未知內部值的估值。
◦ 沿著上緣的邊界條件:
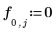
◦ 沿著下緣的邊界條件:
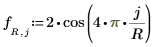
◦ 沿著邊緣的邊界條件:
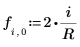
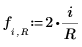
6. 定義 Jacobi spectral radius 變數 r,這是介於 0 與 1 之間的實數。
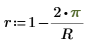
此參數可控制演算法的收斂度。若您看到錯誤訊息「太多疊代」,請嘗試降低 r。 |
7. 呼叫 relax 函數:
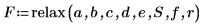
8. 建立 3D 繪圖,顯示方形平板上的熱分佈。
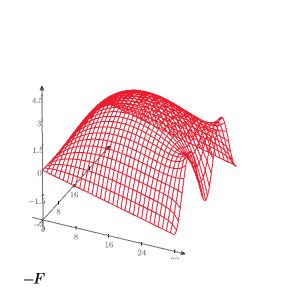
9. 建立等高線圖,顯示固定溫度線。