範例:正轉換 dft
使用 dft 函數求解實數或複數向量或任意大小的矩陣之複數傅立葉轉換,而樣本間有常數時間或間距。
1-D 複數正弦數據
在樣本間距 T 建立有 N 個數據點的模擬複數數據集。
1. 定義數據點數。
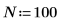
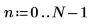
2. 定義採集樣本的時間 T。
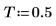
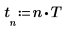
3. 設定角頻率。
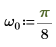
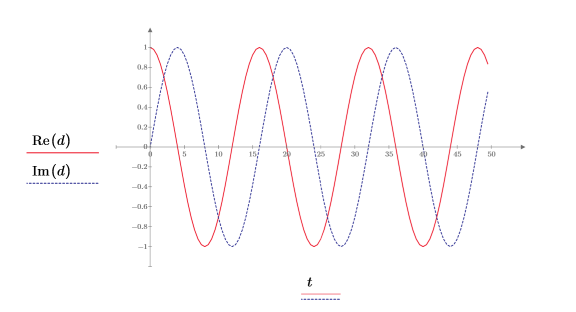
4. 使用 exp 函數定義指數函數。
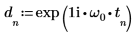
6. 套用 dft 函數,將數據轉換成頻域。
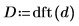
7. 將 D 的絕對值集中在新陣列中。
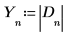
8. 定義取樣頻率及對應至已轉換向量內第 n 項的頻率。
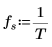
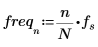
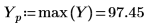
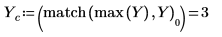
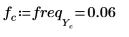
10. 繪製轉換的向量,並使用垂直與水平標記標示幅度達到最大值時的頻率。
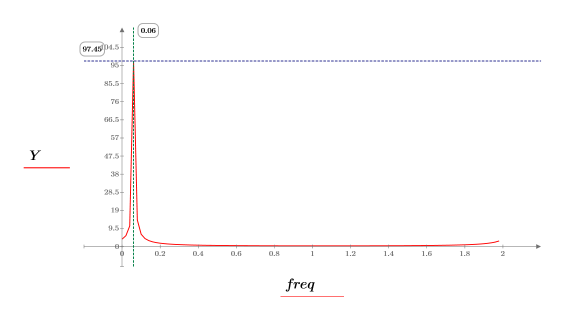
◦ 上半部的頻域樣本代表負頻。
◦ 此複數信號沒有負頻內容。
其他資訊
• 就實數數據向量 v 而言,向量 dft(v) 一般是有關中間值的複數及共軛對稱。在實數矩陣的情況下,得出的每一欄都是共軛對稱。
• 對任何正方形矩陣輸入 A 而言,dft(A) 都是對稱的。
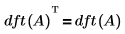
• 根據奈奎斯特取樣定理,取樣頻率至少必須是您希望以傅立葉轉換分解之最高頻率的兩倍。
• 當數據點數目是很大的質數時,快速傅立葉轉換所使用的質因數演算法會變慢。您可能永遠不會碰到此問題,但若需使用極大質數數目的數據點時,務請謹記在心。