數據的離散傅立葉轉換
• dft(A), idft(Z)—傳回複值向量或矩陣的傅立葉轉換或傅立葉逆轉換。
如果 dft 的輸入是長度 r 的向量 V,則:
◦ dft(V) 的輸出是長度 r 的向量 Z
◦ idft(Z) 的輸出是長度 r 的向量
如果 dft 的輸入是具有 r 列和 c 欄的矩陣 M,則:
◦ dft(M) 的輸出是具有 r 列和 c 欄的矩陣 P
◦ idft(P) 的輸出是具有 r 列和 c 欄的矩陣。
• dftr(B)、idftr(Z)—傳回實值向量或矩陣的傅立葉正/逆轉換。
如果 dftr 的輸入是長度 r 的向量 V,則:
◦ dftr(V) 的輸出是長度 Z 的向量 L,其中 L=floor(r/2)+1。Z 的元素與 dft(V) 輸出的第一個 L 元素完全相同。
◦ idftr(Z) 的輸出是長度 r=2(L-1) 的向量。
如果 dftr 的輸入是具有 r 列和 c 欄的矩陣 M,則:
◦ dftr(M) 的輸出是具有 P 列和 r 欄的矩陣 L,其中 L=floor(c/2)+1。P 的元素與·dft(M)·輸出的第一 L·欄完全相同。
◦ idftr(P) 的輸出是具有 r 列和 c=2(L-1) 欄的矩陣。
引數
• A 是任何大小的複值向量或矩陣
• B 是實數向量或矩陣。任何虛數部分都會遭到忽略。如果 B 是向量,則列數必須是 2 的倍數。如果 B 是矩陣,則欄數必須是 2 的倍數
• 對於 A 和 B,數據必須具有相容單位
向量的傅立葉轉換
• 若 A 是大小為 m 的向量,則向量 A 之一維 (1D) 正轉換的第 u 個元素得自 Zu,如下所示:
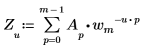
其中:
◦ m 是列數,且 u 定義為: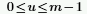
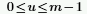
◦ i 是虛數單位,且 wm 定義為:
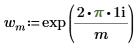
計算以上定義中的 Z 等同於將 dft 函數套用至向量 A。
• 若 Z 是大小為 m 的向量,則向量 Z 之一維 (1D) 逆轉換的第 u 個元素得自 Au,如下所示:
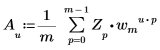
其中:
◦ m、u 及 wm 的定義如上。
計算以上定義中的 A 等同於將 idft 函數套用至向量 Z。
矩陣的傅立葉轉換
• 若 A 是大小為 mxn 的矩陣,則矩陣 A 之二維 (2D) 正轉換的第 (u,v) 個元素得自 Zu,v,如下所示:
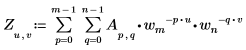
其中:
◦ m、u 及 wm 的定義如上。
◦ n 是欄數,且 v 定義為: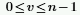
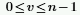
◦ i 是虛數單位,且 wn 定義為:
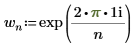
計算以上定義中的 Z 等同於將 dft 函數套用至矩陣 A。
• 若 Z 是大小為 mxn 的矩陣,則矩陣 A 之二維 (2D) 逆轉換的第 (u,v) 個元素得自 Au,v,如下所示:
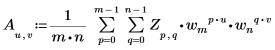
其中:
◦ m、n、u、v、wm 及 wn 的定義如上。
計算以上定義中的 A 等同於將 idft 函數套用至矩陣 Z。
其他資訊
• 當向量的列數及矩陣的欄數為 2 的次方時,傅立葉函數的執行速度會更快。
• 新的 dft/idft 數會取代已過時的 cfft/icfft 和 CFFT/ICFFT 函數的功能,並大幅改善效能,特別是大型數據集與大小不是 2 的倍數之情況。
• 新的 dftr/idftr 函數會取代已過時的 fft/ifft 和 FFT/IFFT 函數的功能。
函數 dftr 會在長度為偶數的實數向量上運算,並在具有偶數欄數的矩陣上運算。
• 函數 fft/FFT 只會在長度為 2 的次方的實數向量上運算。
• 函數 ifft/IFFT 只有一半是輸入向量長度加一,或是 2k-1+1,其中 k 為 > 1 的整數。您必須手動重新建構另一半 (第一部分的共軛部分但順序相反)。函數 dft/idft 會傳回完整的結果。
• 函數 dft/idft 的比例係數和指數正負號,與已過時的 fft/ifft、FFT/IFFT 及 cfft/icfft、CFFT/ICFFT 皆不同。
◦ 正轉換的差異包括:
dft/dftr | fft/cfft | FFT/CFFT | |
|---|---|---|---|
比例係數 | 1 | 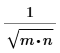 | 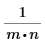 |
指數正負號 | 負數 | 正數 | 負數 |
◦ 逆轉換的差異包括:
idft/idftr | ifft/icfft | IFFT/ICFFT | |
|---|---|---|---|
比例係數 | 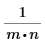 | 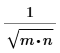 | 1 |
指數正負號 | 正數 | 負數 | 正數 |
為僅在向量上運算之函數 (1D 的情況) 計算比例係數時,會假設 n=1。