示例:配合使用单位和多项式插值函数
1. 定义两个输入矢量和一个独立变量。
 |
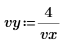 |
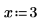 |
2. 定义单位。
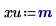
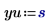
3. 计算输入矢量和输入变量。
 |  | 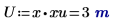 |
独立变量 U 单位必须与第一个自变量矢量单位匹配。 |
多项式插值
1. 使用 polyint 函数计算在指定的独立变量值处的插值函数。
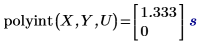
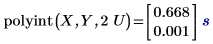
在输入矢量 X 中查看 U 会找到一个匹配,且在矢量 Y 中的对应精确值为 1.333 (零误差)。但是,2U 在 X 中不具有精确匹配,从而导致出现带有非零误差的插值。
2. 使用函数 length 确定输入矢量的长度,然后创建一个短程序计算在不同点处的插值函数。在第一列显示插值点,在第二列显示误差值。
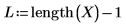

变量 u 必须为标量,并且将单位 m 添加为函数自变量的一部分。
3. 将插值点和误差值保存到两个单独的矢量中。
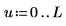
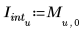
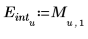
4. 绘制带有误差包络的插值点。
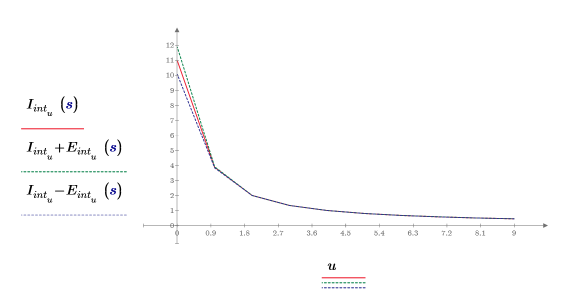
误差开始时相对较大,但在第二个插值点后变小 (几乎可以忽略)。
多项式迭代
1. 使用 polyiter 函数计算在指定的独立变量值、最大迭代次数和公差处的迭代函数。
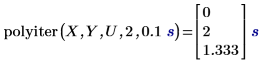
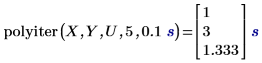
• 如果数据点的最后两个迭代估值在公差值的范围内一致或迭代次数达到允许的最大迭代次数,算法将停止。 • 第一个结果显示了迭代函数在达到允许的最大两次迭代次数后收敛失败,因此其返回矢量 Y 中的相应元素。 • 第二个结果显示了迭代函数在第三次迭代后进行了收敛,并且没有达到允许的最大五次迭代次数。 |
2. 使用一个短程序计算在十个不同点处的迭代函数。使用函数 augment 将误差值添加到返回矩阵的第四列中,其中第一列显示合并状态,第二列显示利用的迭代次数,第三列显示迭代值。

3. 将插值点和误差值保存到单独的矢量中。
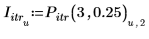
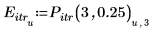
4. 绘制 3 次迭代且误差为 0.25 的迭代点。
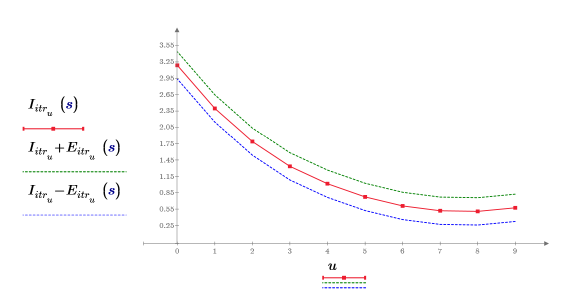
误差在每个插值点处为常数。
5. 将最大迭代次数设置为 3 和误差设置为 0.25 后,比较插值和迭代的返回结果。
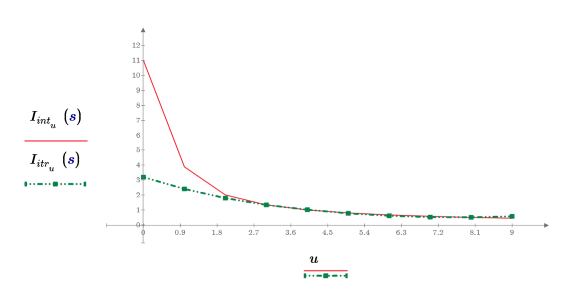
6. 显示了将迭代次数设置为较大数以及误差设置为零时,插值结果与迭代结果相同。
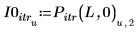
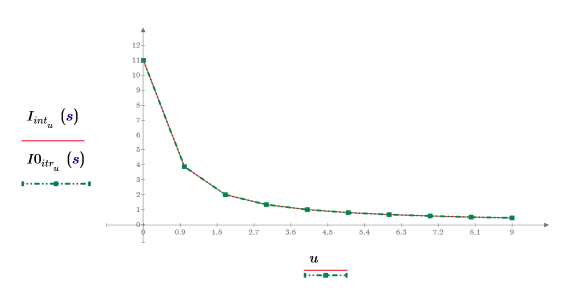
最大迭代次数必须小于输入矢量的长度。