示例:使用极限运算符
使用无穷大作为极限值
1. 当表达式的自变量接近无穷大时,使用极限运算符并以符号方式计算表达式。
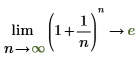
2. 绘制函数的图象,以使其可视化。使用水平标记表示 e。
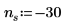 | 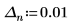 | 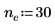 |
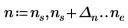 | ||
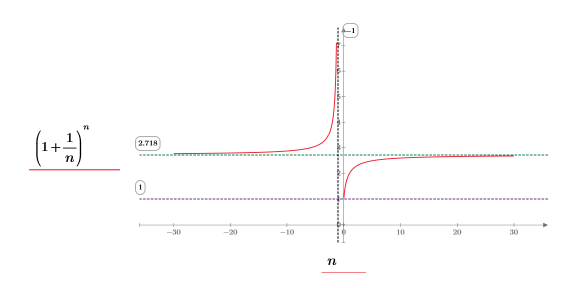 | ||
在 (x, y) 象限,我们观察到以下内容:
◦ 当 n 接近 positive infinity 时,函数接近 y=e。
◦ 当 n 接近 0 时,函数接近 y=1。
从数学上讲,这些情况可由以下符号运算表示:
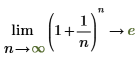 | 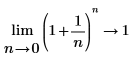 |
在 (-x, y) 象限,我们观察到以下内容:
◦ 当 n 接近 negative infinity 时,函数接近 y=e。
◦ 当 n 接近 -1 时,函数接近 y=infinity。
从数学上讲,这些情况可由以下符号运算表示:
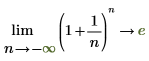 | 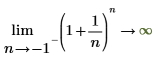 |
在第二个方程中使用左侧极限侧意味着从曲线的左侧接近 -1。如果未指定,则运算会因为未将函数定义为 -1 < n < 0 而返回“undefined (未定义)”: 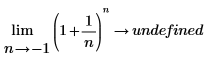 |
使用极限侧
1. 绘制 cot 函数图像。
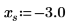 | 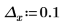 | 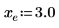 |
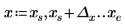 | ||
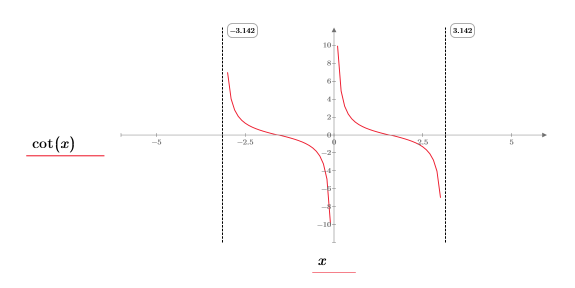 | ||
在 (x, y) 象限,我们观察到以下内容:
◦ 当 x 接近 0 时,函数接近 y=infinity。
◦ 当 x 接近 π 时,函数接近 y=-infinity。
从数学上讲,这些情况可由以下符号运算表示:
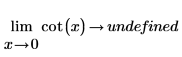 | 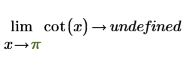 |
因为该函数关于 x=+/- n*π/2 对称,所以符号运算会因函数在 x=0 (和 π 的任意倍数) 附近可能为 infinity 或 -infinity 而返回“undefined (未定义)”,具体取决于 x 从哪一侧趋近 0。
这是关于指定“极限侧”的一个不错的示例。
2. 指定“极限侧”并以符号方式重新计算 0 和 π 附近的函数 cot。
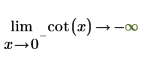 | 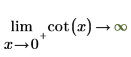 |
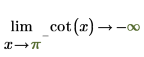 | 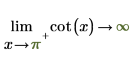 |
返回的结果与绘图一致。
有时为可视化函数和复查符号运算结果的有效性而绘制函数图象会很有帮助。 |