示例:符号微积分 II
通过使用符号求值运算符计算问题的表达式来解决微积分中的符号问题,并在需要时添加关键字来修改问题。
泰勒和麦克劳林级数
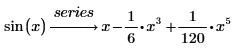
默认设置下,PTC Mathcad 返回最高第 6 阶的项,因而答案中最高的乘方为 5。 |
2. 在 series 后键入逗号,然后在占位符中键入 x, 10 将项的阶增加至 10。
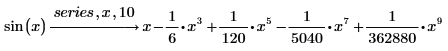
3. 关于 1 以泰勒级数展开 sin 函数。
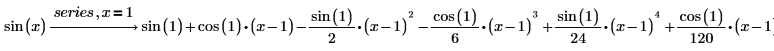
4. 围绕点 (x, y)=(0, 1) 以多个变量展开函数。
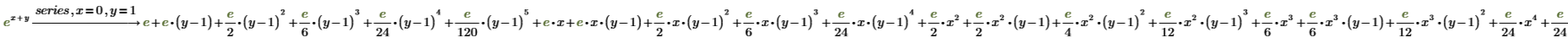
5. 将系数显示为四位数,而不是显示为 e。
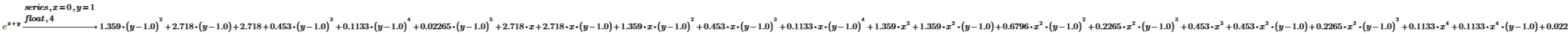
部分分式
1. 使用关键字 parfrac 执行有理函数 (多项式的商) 的部分分式分解。
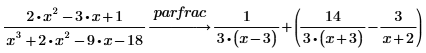
2. 对通过值域求积运算符定义的函数进行部分分式分解。
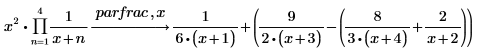
对实数或复数进行分解
默认情况下,PTC Mathcad 对有理数的域执行部分分式分解。即如果初始表达式为具有有理系数的多项式的商,则结果中的多项式也将拥有有理系数。
1. 使用关键字 parfrac 来查找以下函数的分式。
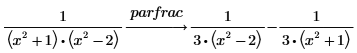
2. 在以下表达式中对其中一项进行进一步分解:
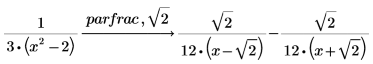
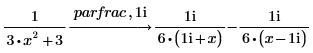
3. 在 parfrac 后键入 domain = complex 通过复数对有理函数进行完全部分分式分解。
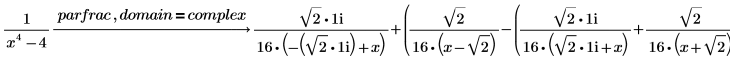
执行步骤对实数进行分解: a. 使用关键字 simplify,将最后两项合并为带实数系数的一项,如下所示: 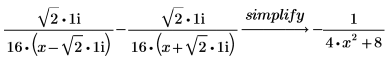 b. 用简化的结果替换原始结果来获取以下结果: 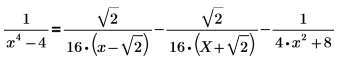 |
连分式
1. 使用关键字 confrac 来查找数字的连分式展开。
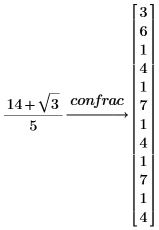
2. 使用修饰符 fraction 来查看实际的连分式而不是矢量。
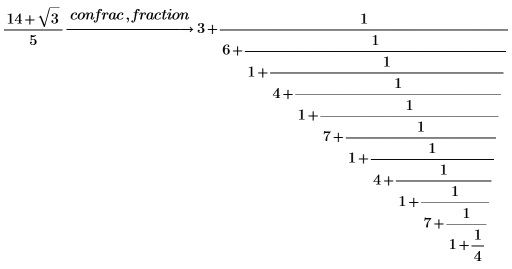
默认情况下,PTC Mathcad 会返回足够的连分式项,因而解可精确到 10 位有效数字。 |
3. 可添加指定有效位数的正整数,以不同的精确度返回结果。
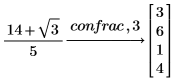

4. 将函数 sin 展开为连分式。
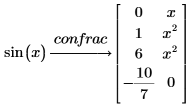
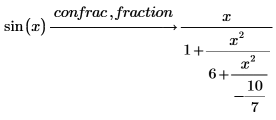
PTC Mathcad 返回包含与各项对应的 x 的乘方的第二列。 |