示例:线性回归
使用 polyfitc、line、slope 和 intercept 函数在 x-y 数据集中查找最佳拟合的最小二乘线。使用 stderr 函数计算拟合参数中的误差。计算最佳拟合线周围的置信限并形成置信区间。
最佳拟合线
创建线性函数以估算行驶不同距离需用的时间。
1. 定义距离集 (以米计) 和行驶这些距离需用的时间 (以分计)。
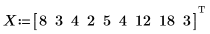
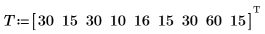
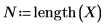
2. 定义一元线性回归方程。
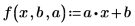
3. 调用 polyfitc 计算回归方程的系数 a 和 b。
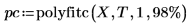
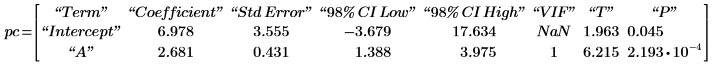

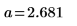
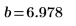
4. 定义从各个点到线距离的平方和最小化的最佳拟合线。
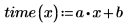
应仅对趋近于原始观察数据的值使用线性回归或其他类型回归的参数化方程。以上数据的最佳拟合线预测,将需用下列时间行进 0 米的距离:
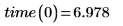
这在测量时间必须为恒定速度下的行程时间时并不符合逻辑。这种结果有时可以表示特定的物理现象。此种情况下,行驶零米所需的时间可解释为在交通灯处的平均等待时间。
5. 绘制数据点和最佳拟合线。
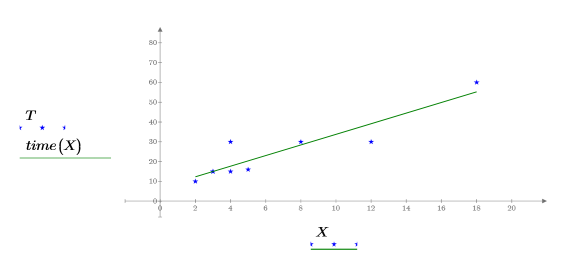
计算斜率和截距的可选方法
计算最佳拟合线的斜率和截距有多种方法。例如,line 函数结合 slope 和 intercept 函数。其他方法包括矩阵计算或统计关系。
1. 调用 intercept 和 slope 函数。
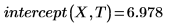
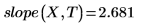
2. 调用 line 函数。
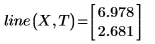
3. 通过使用 augment 函数来使用矩阵计算。
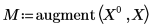
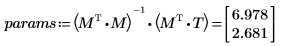
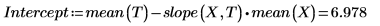
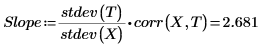
5. 用图像显示最小二乘线始终经过 (mean(X), mean(T)) 点:
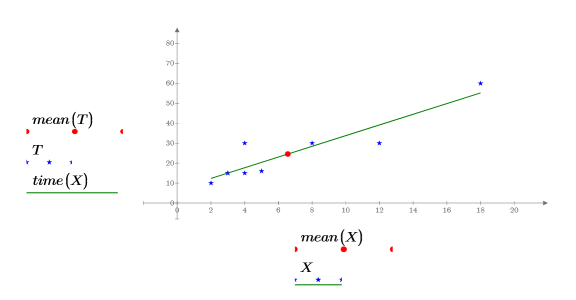
标准误差
计算估计标准误差 (也称为标准误差) 以衡量以上线性拟合的程度。同样,计算斜率和截距的误差。
1. 定义自由度 (数据点数与拟合参数数的差值)。
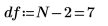
2. 调用 stderr 函数计算以上定义的最佳拟合线的估计标准误差。
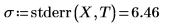
此为均方误差 MSE 或 σ2 的平方根:
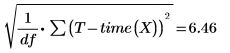
3. 比较计算所得的标准误差与 polyfitstat 函数所返回的标准误差。
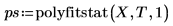
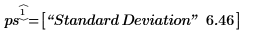
4. 计算斜率和截距的标准误差。
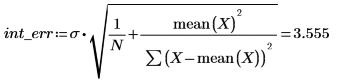
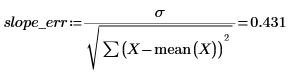
5. 使用矩阵计算重复上面的运算。
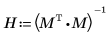
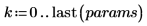
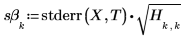
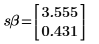
6. 使用 augment 函数显示每个回归系数的标准误差记录在 polyfitc 函数所返回的矩阵中。
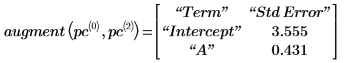
各个系数的置信区间
使用以上估值连同 t 分布中的百分比点,形成斜率和截距估值的置信区间。
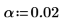
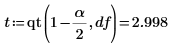
2. 计算斜率的置信限。
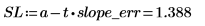
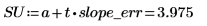
实际斜率值落在 SL 和 SU 之间,这种情况存在的可能性为 98%。
3. 计算截距的置信限。
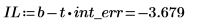
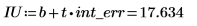
该值的宽广范围反映数据中的高程度散点。
4. 调用 confidence 函数重复步骤 1 至 3。
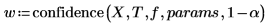
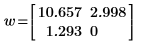
confidence 函数的第一列中返回置信区间宽度,第二列中返回 t 因子。用宽度除以 t 因子时,将重新获得这两个参数的标准误差:
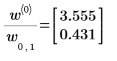
5. 要求置信限,可用相关参数加上或减去宽度:
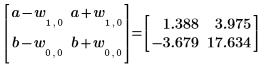
6. 使用 augment 函数显示每个回归系数的标准误差记录在 polyfitc 函数所返回的矩阵中。

回归的置信区间
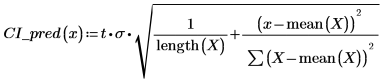
2. 使用上面函数来计算任一预测 x 值的置信区间。
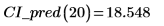
3. 使用矩阵计算:
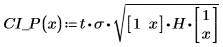
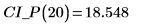
4. 绘制整个回归区域的数据、最佳拟合线和置信区间的图像。
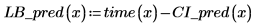
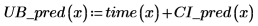
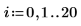
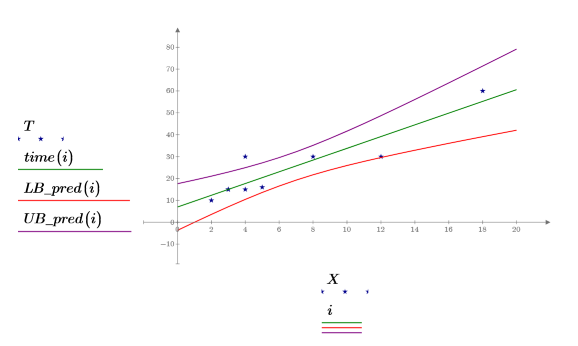
预测值的置信区域在测量值的中心附近变窄。由于用来计算回归的公式基于均值,因此离数据均值越近,预测值越准确。
5. 计算测量值的置信限。这些置信限与预测值的置信限稍有不同。
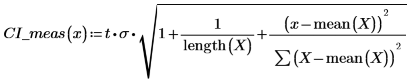
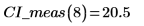
6. 使用矩阵计算:
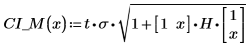
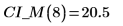
7. 将置信限绘制为误差图轨迹。
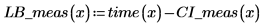
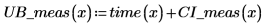
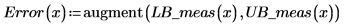
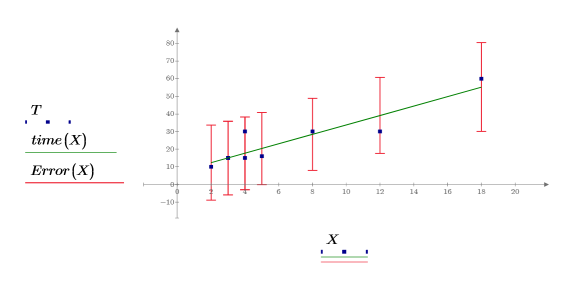
可将这些图用作离群值检测,其中落在置信区间以外的测量值表示离群值。 |