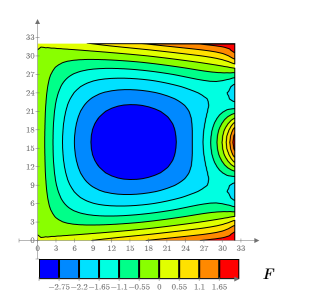
示例:方形板上的热流 - II
使用偏微分方程求解器 relax 求解方形板的稳态温度分布。
求解泊松方程
在已知源函数值和边界条件不为零的条件下求解热方程。
|
|
relax 函数基于完全不同的求解方法,因此需要不同的自变量集。
|
1. 定义五个含有拉普拉斯近似系数的方阵a、b、c、d 和 e:
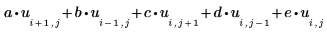
这些数组可以具有指定的任意大小。这些数组越大,则解中的网格越精细。 |
2. 定义方形板的维数:
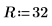
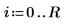
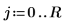
3. 定义系数:
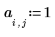
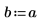
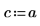
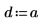
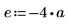
4. 定义常数源的强度和位置。
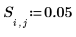
5. 定义一个包含已知函数 F(x,y) 的边界值和未知内部值的估值的方阵 f,其大小与网格大小相同。
◦ 沿顶部的边界条件:
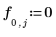
◦ 沿底部的边界条件:
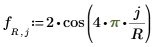
◦ 沿边缘的边界条件:
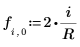
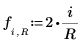
6. 定义 Jacobi spectral radius 变量 r,一个介于 0 和 1 之间的实数。
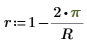
该参数控制算法的收敛度。如果看到错误消息“迭代次数太多”,则尝试减小 r 值。 |
7. 调用 relax 函数:
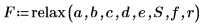
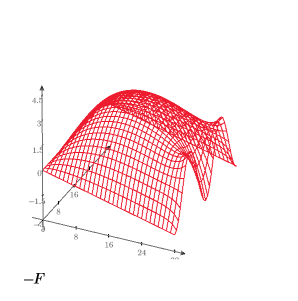
8. 创建 3D 绘图来显示方形板上的热分布。
9. 创建等值线图来显示恒温线。