示例:正变换 dft
使用 dft 函数求得样本之间具有恒定时间或空间的任何大小的实 (或复) 数值矢量或矩阵的复数形式傅立叶变换。
1-D 复数正弦数据
创建具有 N 个采样间隔为 T 的数据点的模拟复数数据集。
1. 定义数据点的数量。
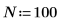
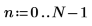
2. 定义样本收集时间 T。
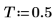
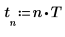
3. 设置角频率。
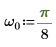
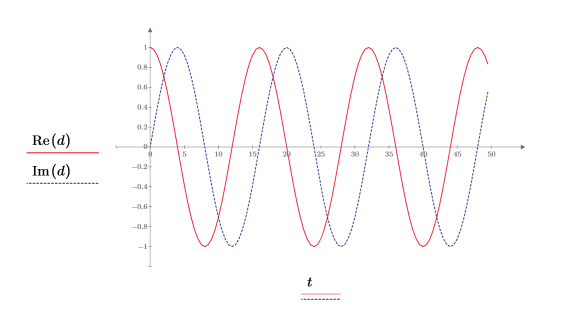
4. 使用 exp 函数来定义指数函数。
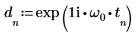
6. 应用 dft 函数将数据变换为频域。
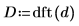
7. 将 D 的绝对值收集至新数组。
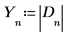
8. 定义采样频率以及对应于已变换矢量中第 n 个条目的频率。
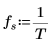
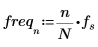
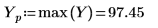
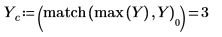
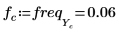
10. 绘制已变换矢量的图像,并使用竖直和水平标记来标记振幅为最大值时的频率。
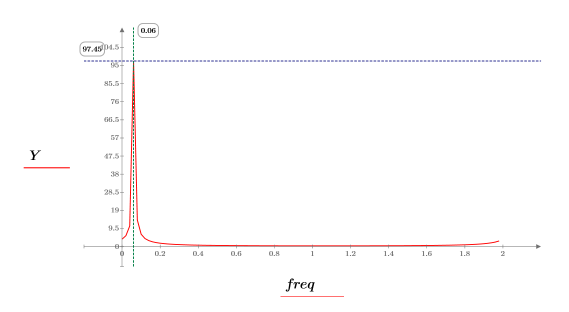
◦ 频域样本的上半部分表示负频率。
◦ 复信号不具有负频谱。
附加信息
• 对于实数据矢量 v,矢量 dft(v) 通常关于中值呈复共轭对称。对于实数矩阵来说,结果的每列都呈共轭对称。
• 对于任意方阵列输入 A,dft(A) 是对称的。
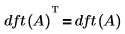
• 根据尼奎斯特采样定理,采样频率最小必须为通过傅立叶变换求解所期望得到的最高频率的二倍。
• 数据点的数目是较大的质数时,快速傅立叶变换中使用的质因子算法的速度将放慢。您可能从来不会遇到此问题,但如果您需要使用的数据点数目是很大的质数,则应该对此问题有所了解。