첨도 및 비대칭도
• kurt(A, B, C, ...) - 요소 A, B, C, ...의 첨도를 구합니다. 첨도는 다음과 같이 정의됩니다.
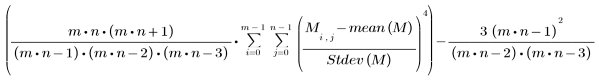
값 집합의 첨도는 정규 분포와 비교할 때 분포가 얼마나 평평한지 혹은 뾰족한지를 나타냅니다.
값 | 분포 형태 |
|---|---|
kurt = 0 | 정규 분포 |
kurt > 0 | 상대적으로 뾰족한 분포 |
kurt < 0 | 상대적으로 평평한 분포 |
• skew(A, B, C, ...) - 요소 A, B, C, ...의 비대칭도를 구합니다. 비대칭도는 다음과 같이 정의됩니다.
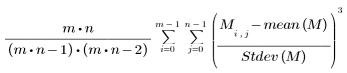
값 집합의 비대칭도는 평균을 중심으로 비대칭성을 측정합니다.
값 | 분포 형태 |
|---|---|
skew = 0 | 이 분포는 정규 분포와 마찬가지로 평균을 중심으로 대칭입니다. |
skew > 0 | 분포 "꼬리"가 양의 값을 향해 확장됩니다. |
skew < 0 | 분포 "꼬리"가 음의 값을 향해 확장됩니다. |
인수
• A, B, C, ...는 스칼라 값이거나 배열입니다. 인수의 요소는 kurt의 경우 4개 이상, skew의 경우 3개 이상 있어야 합니다.
• M은 함수 인수 A, B, C, ...에서 생성된 배열입니다. M의 표준 편차는 0이 아니어야 합니다.